(1)在一个红绿灯路口,红灯、黄灯和绿灯的时间分别为30秒、5秒和40秒.当你到达路口时,求不是红灯的概率.
(2)已知关于x的一元二次函数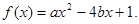 设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为
设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为 和
和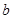 ,求函数
,求函数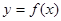 在区间[
在区间[ 上是增函数的概率.
上是增函数的概率.
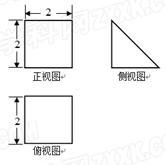
(本小题满分14分)三棱柱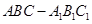 的直观图及三视图(正视图和俯视图是正方形,侧视图是等腰直角三角形)如图所示,
的直观图及三视图(正视图和俯视图是正方形,侧视图是等腰直角三角形)如图所示,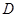 为
为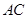 的中点.
的中点.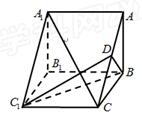
(1)求证: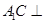 平面
平面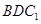 ;
;
(2)求二面角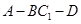 的正切值.
的正切值.
(本小题满分12分) 惠州市某校中学生篮球队假期集训,集训前共有6个篮球,其中3个是新球(即没有用过的球),3个是旧球(即至少用过一次的球).每次训练都从中任意取出2个球,用完后放回.
(1)设第一次训练时取到的新球个数为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(2)已知第一次训练时用过的球放回后都当作旧球,求第二次训练时恰好取到 个新球的概率.
个新球的概率.
参考公式:互斥事件加法公式: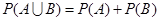 (事件
(事件 与事件
与事件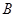 互斥).
互斥).
独立事件乘法公式: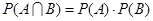 (事件
(事件 与事件
与事件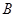 相互独立).
相互独立).
条件概率公式: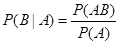 .
.
(本小题满分12分)已知函数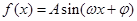 ,
,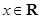 (其中
(其中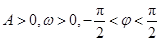 ),其部分图像如图所示.
),其部分图像如图所示.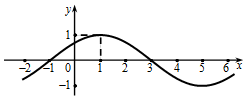
(1)求函数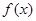 的解析式;
的解析式;
(2)已知横坐标分别为 、
、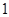 、
、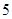 的三点
的三点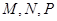 都在函数
都在函数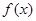 的图像上,求
的图像上,求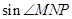 的值.
的值.
(本小题满分13分)对于函数 ,如果它们的图象有公共点P,且在点P处的切线相同,则称函数
,如果它们的图象有公共点P,且在点P处的切线相同,则称函数 和
和 在点P处相切,称点P为这两个函数的切点.设函数
在点P处相切,称点P为这两个函数的切点.设函数 ,
, .
.
(Ⅰ)当 ,
, 时,判断函数
时,判断函数 和
和 是否相切?并说明理由;
是否相切?并说明理由;
(Ⅱ)已知 ,
, ,且函数
,且函数 和
和 相切,求切点P的坐标;
相切,求切点P的坐标;
(Ⅲ)设 ,点P的坐标为
,点P的坐标为 ,问是否存在符合条件的函数
,问是否存在符合条件的函数 和
和 ,使得它们在点P处相切?若点P的坐标为
,使得它们在点P处相切?若点P的坐标为 呢?(结论不要求证明)
呢?(结论不要求证明)
(本小题满分14分)已知椭圆C: 的右焦点为F,右顶点为A,离心率为e,点
的右焦点为F,右顶点为A,离心率为e,点 满足条件
满足条件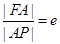 .
.
(Ⅰ)求m的值;
(Ⅱ)设过点F的直线l与椭圆C相交于M,N两点,记 和
和 的面积分别为
的面积分别为 ,
,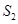 ,若
,若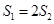 ,求直线l的方程.
,求直线l的方程.