(本小题满分13分)对于函数 ,如果它们的图象有公共点P,且在点P处的切线相同,则称函数
,如果它们的图象有公共点P,且在点P处的切线相同,则称函数 和
和 在点P处相切,称点P为这两个函数的切点.设函数
在点P处相切,称点P为这两个函数的切点.设函数 ,
, .
.
(Ⅰ)当 ,
, 时,判断函数
时,判断函数 和
和 是否相切?并说明理由;
是否相切?并说明理由;
(Ⅱ)已知 ,
, ,且函数
,且函数 和
和 相切,求切点P的坐标;
相切,求切点P的坐标;
(Ⅲ)设 ,点P的坐标为
,点P的坐标为 ,问是否存在符合条件的函数
,问是否存在符合条件的函数 和
和 ,使得它们在点P处相切?若点P的坐标为
,使得它们在点P处相切?若点P的坐标为 呢?(结论不要求证明)
呢?(结论不要求证明)
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上 件产品作为样本称出它们的重量(单位:克),重量的分组区间为
件产品作为样本称出它们的重量(单位:克),重量的分组区间为 ,
,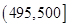 , ,
, ,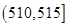 ,由此得到样本的频率分布直方图,如图所示.
,由此得到样本的频率分布直方图,如图所示.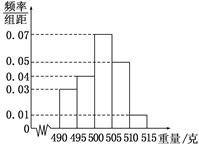
(1)根据频率分布直方图,求重量超过 克的产品数量;
克的产品数量;
(2)在上述抽取的 件产品中任取
件产品中任取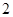 件,设
件,设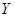 为重量超过
为重量超过 克的产品数量,求
克的产品数量,求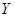 的分布列;
的分布列;
(3)从该流水线上任取 件产品,求恰有
件产品,求恰有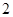 件产品的重量超过
件产品的重量超过 克的概率.
克的概率.
设向量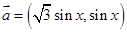 ,
, ,
,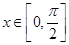 .
.
(1)若 ,求
,求 的值;
的值;
(2)设函数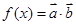 ,求
,求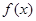 的最大值.
的最大值.
(本小题满分14分)设函数 ,
,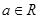 且
且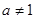 . 曲线
. 曲线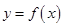 在点
在点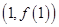 处的切线的斜率为
处的切线的斜率为 .
.
(1)求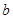 的值;
的值;
(2)若存在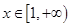 ,使得
,使得 ,求
,求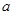 的取值范围.
的取值范围.
(本小题满分14分)已知椭圆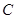 过点
过点 ,点
,点 是椭圆的左焦点,点
是椭圆的左焦点,点 、
、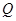 是椭圆
是椭圆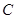 上的两个动点,且
上的两个动点,且 、
、 、
、 成等差数列.
成等差数列.
(1)求椭圆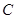 的标准方程;
的标准方程;
(2)求证:线段 的垂直平分线经过一个定点
的垂直平分线经过一个定点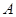 .
.
(本小题满分14分)已知数列 的前
的前 项和为
项和为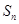 ,且满足
,且满足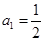 ,
, (
(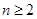 且
且 ).
).
(1)求证:数列 是等差数列;
是等差数列;
(2)求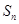 和
和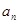 .
.