为改善城市生态环境,实现城市生活垃圾减量化、资源化、无害化的目标,湖州市决定从2010年12月1日起,在全市部分社区试点实施生活垃圾分类处理. 某街道计划建造垃圾初级处理点20个,解决垃圾投放问题. 有A、B两种类型处理点的占地面积、可供使用居民楼幢数及造价见下表:
| 类型 |
占地面积/m2 |
可供使用幢数 |
造价(万元) |
| A |
15 |
18 |
1.5 |
| B |
20 |
30 |
2.1 |
已知可供建造垃圾初级处理点占地面积不超过370m2,该街道共有490幢居民楼.
(1)满足条件的建造方案共有几种?写出解答过程.
(2)通过计算判断,哪种建造方案最省钱,最少需要多少万元.
已知:关于 的方程
的方程 有两个不相等的实数根.
有两个不相等的实数根.
(1)求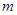 的取值范围;
的取值范围;
(2)抛物线 :
: 与
与 轴交于
轴交于 、
、 两点.若
两点.若 且直线
且直线 :
: 经过点
经过点 ,求抛物线
,求抛物线 的函数解析式;
的函数解析式;
(3)在(2)的条件下,直线 :
: 绕着点
绕着点 旋转得到直线
旋转得到直线 :
: ,设直线
,设直线 与
与 轴交于点
轴交于点 ,与抛物线
,与抛物线 交于点
交于点 (
( 不与点
不与点 重合),当
重合),当 时,求
时,求 的取值范围.
的取值范围.
生活中,有人用纸条可以折成正五边形的形状,折叠过程是将图①中的纸条按图②方式拉紧,压平后可得到图③中的正五边形(阴影部分表示纸条的反面).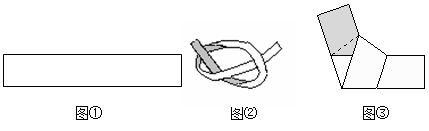
(1)将 两端剪掉则可以得到正五边形
两端剪掉则可以得到正五边形 ,若将
,若将 展开,展开后的平面图形是;
展开,展开后的平面图形是;
(2)若原长方形纸条(图①)宽为2cm,求(1)中展开后平面图形的周长(可以用三角函数表示).
图①表示的是石景山某商场2012年前四个月中两个月的商品销售额的情况,图②表示的是商场家电部各月销售额占商场当月销售总额的百分比情况,观察图①、图②解答下列问题:
(1)商场前四个月财务结算显示四月份商场的商品销售额比一月份下降了20%,请你求出商场四月份的销售额;
(2)若商场前四个月的商品销售总额一共是500万元,请你根据这一信息将图①中的统计图补充完整;
(3)小明观察图②后认为,商场家电部四月份的销售额比三月份减少了,你同意他的看法吗?请你说明理由.
如图,AB是⊙ 的直径,弦CD与AB交于点E,过点
的直径,弦CD与AB交于点E,过点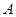 作⊙
作⊙ 的切线与
的切线与 的延长线交于点
的延长线交于点 ,如果
,如果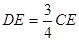 ,
,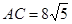 ,
, 为
为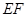 的中点.
的中点.
(1)求证: ;
;
(2)求AB的长.
如图,在直角梯形ABCD中,AB∥DC,AB⊥BC,∠A=60°,AB=2CD,E、F分别为AB、AD的中点,联结EF、EC、BF、CF.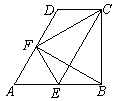
(1)四边形AECD的形状是;
(2)若CD=2,求CF的长.