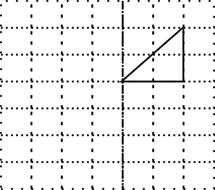
如图为7×7的正方形网格,
(1)作出等腰直角三角形ABC关于直线MN成轴对称变换的像⊿A1BC1(A对应A1,C对应C1);
(2)作出⊿A1BC1绕点B逆时针旋转90o得到的像⊿A2BC2(A1对应A2, C1对应C2);
(3)填空:⊿A2BC2可以看作将⊿ABC经过连续两次平移得到,则这两次平移具体的操作方法是 ____________________________(需指明每次平移的方向和距离).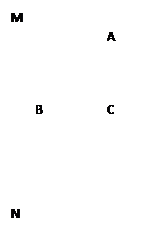
如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.
(1) 试判断BE与FH的数量关系,并说明理由;
(2) 求证:∠ACF=90°;
(3) 连接AF,过A,E,F三点作圆,如图2. 若EC=4,∠CEF=15°,求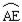 的长.
的长.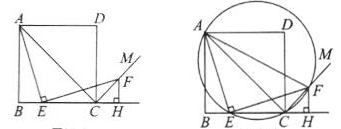
图1图2
“保护好环境,拒绝冒黑烟”.某市公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆. 若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1) 求购买A型和B型公交车每辆各需多少万元?
(2) 预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次. 若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客量总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案的总费用最少?最少总费用是多少?
如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.
(1) 求证:△ADE≌△CFE;
(2) 若GB=2,BC=4,BD=1,求AB的长.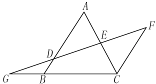
考试前,同学们总会采用各种方式缓解考试压力,以最佳状态迎接考试. 某校对该校九年级的部分同学做了一次内容为“最适合自己的考前减压方式”的调查活动,学校将减压方式分为五类,同学们可根据自己的情况必选且只选其中一类,学校收集整理数据后,绘制了图1和图2两幅不完整的统计图,请根据统计图中的信息解答下列问题:
(1)这次抽样调查中,一共抽查了多少名学生?
(2)请补全条形统计图;
(3)请计算扇形统计图中“享受美食”所对应扇形的圆心角的度数;
(4)根据调查结果,估计该校九年级500名学生中采用“听音乐”的减压方式的人数.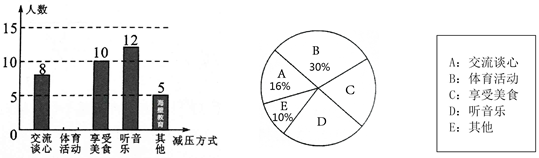
图1图2
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A B
B C
C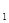 ;
;
(2) 请画出△ABC关于原点对称的△A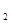 B
B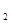 C
C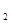 ;
;
(3) 在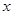 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.