深化理解(本小题满分9分)
如图,在平面直角坐标系中,点C的坐标为(0,4),A是 轴上的一个动点,M是线段AC的中点.把线段AM进行以A为旋转中心、向顺时针方向旋转90°的旋转变换得到AB.过B作
轴上的一个动点,M是线段AC的中点.把线段AM进行以A为旋转中心、向顺时针方向旋转90°的旋转变换得到AB.过B作 轴的垂线、过点C作
轴的垂线、过点C作 轴的垂线,两直线交于点D,直线DB交
轴的垂线,两直线交于点D,直线DB交 轴于一点E.
轴于一点E.
设A点的横坐标为 ,
,
(1)若 =3,则点B的坐标为 ▲ ,若
=3,则点B的坐标为 ▲ ,若 =-3,,则点B的坐标为 ▲ ;
=-3,,则点B的坐标为 ▲ ;
(2)若 >0,△BCD的面积为
>0,△BCD的面积为 ,则
,则 为何值时,
为何值时, ?
?
(3)是否存在 ,使得以B、C、D为顶点的三角形与△AOC相似?若存在,求此时
,使得以B、C、D为顶点的三角形与△AOC相似?若存在,求此时 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
抛物线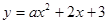
 交
交 轴于
轴于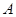 、
、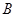 两点,交
两点,交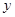 轴于点
轴于点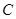 ,顶点为
,顶点为 .
.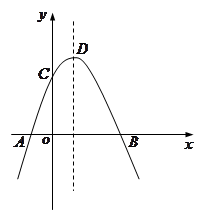
写出抛物线的对称轴及
 、
、 两点的坐标(用含
两点的坐标(用含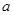 的代数式表示)
的代数式表示)连接
 并以
并以 为直径作⊙
为直径作⊙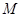 ,当
,当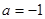 时,请判断⊙
时,请判断⊙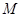 是否经过点
是否经过点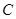 ,并说明理由;
,并说明理由;在(2)题的条件下,点
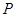 是抛物线上任意一点,过
是抛物线上任意一点,过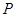 作直线垂直于对称轴,垂足为
作直线垂直于对称轴,垂足为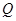 . 那么是否存在这样的点
. 那么是否存在这样的点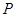 ,使△
,使△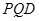 与以
与以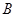 、
、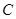 、
、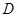 为顶点的三角形相似?若存在,请求出点
为顶点的三角形相似?若存在,请求出点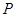 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
宏达纺织品有限公司准备投资开发A、B两种新产品,通过市场调研发现:如果单独投资A种产品,则所获利润(万元)与投资金额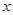 (万元)之间满足正比例函数关系:
(万元)之间满足正比例函数关系: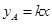 ;如果单独投资B种产品,则所获利润(万元)与投资金额
;如果单独投资B种产品,则所获利润(万元)与投资金额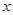 (万元)之间满足二次函数关系:
(万元)之间满足二次函数关系: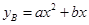 .根据公司信息部的报告,
.根据公司信息部的报告,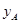 ,
,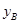 (万元)与投资金额
(万元)与投资金额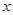 (万元)的部分对应值(如下表)
(万元)的部分对应值(如下表)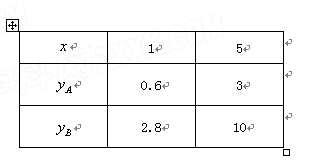
填空:
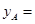 _______________________;
_______________________;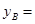 _______________________;
_______________________;如果公司准备投资20万元同时开发A、B两种新产品,设公司所获得的总利润为
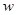 (万元),试写出
(万元),试写出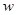 与某种产品的投资金额x之间的函数关系式.
与某种产品的投资金额x之间的函数关系式.请你设计一个在(2)中能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少万元?
一个不透明的口袋里装着红、黄、绿三种只有颜色不同的球,其中红球有2个,黄球有1个,从中任意摸出1球是红球的概率为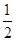 .
.试求袋中绿球的个数;
第1次从袋中任意摸出l球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率
如图,在矩形ABCD中,AB=3cm,AD=4cm,点E是BC上一动点(不与B、C重合),且DF⊥AE,垂足为F. 设AE=xcm,DF=ycm.
求证:△DFA∽△ABE;
试求y与x之间的函数关系式,并求出自变量的取值范围.
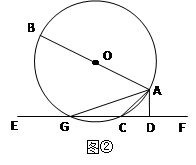
如图①,AB是⊙O的直径,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D。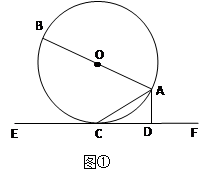
求证:∠DAC=∠BAC;
若把直线EF向上平行移动,如图②,EF交⊙O于G、C两点,若题中的其它条件不变,猜想:此时与∠DAC相等的角是哪一个?并证明你的结论。