某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示).根据图表解答下列问题:
⑴ a= ,b= ;
⑵ 这个样本数据的中位数落在第 组;
⑶ 若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀,则从这50名男生中任意选一人,跳绳成绩为优秀的概率为多少?
⑷ 若该校七年级入学时男生共有150人,请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数.
如图,写出A、B、C关于X轴对称的点坐标,并作出与△ABC关于Y轴对称的图形。
没有量角器,利用刻度尺也能画出一个角的平分线吗?下面是小彬的做法,他的画法正确吗?请说明理由.
如图,角平分线刻度尺画法: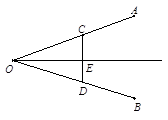
①利用刻度尺在∠AOB 的两边上,分别取OD=OC.
②连结CD,利用刻度尺画出CD的中点E.
③画射线OE.所以射线OE为∠AOB的角平分线.
沿虚线,画出四种不同的图案,分别将下面的正方形划分成两个全等的图形.
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=AC=EF=3,∠BAC=∠DEF=90º,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止.现不考虑旋转开始和结束时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)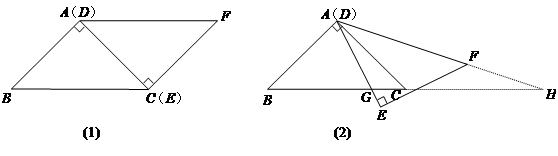
(1)问:始终与△AGC相似的三角形有 及 ;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据图(2)的情形说明理由);
(3)问:当x为何值时,△AGH是等腰三角形。
在“5.12大地震”灾民安置工作中,某企业接到一批生产甲种板材24000 和乙种板材12000
和乙种板材12000 的任务.(1)已知该企业安排140人生产这两种板材,每人每天能生产甲种板材30
的任务.(1)已知该企业安排140人生产这两种板材,每人每天能生产甲种板材30 或乙种板材20
或乙种板材20 .问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
.问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
(2)某灾民安置点计划用该企业生产的这批板材搭建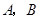 两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间
两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间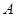 型板房和一间
型板房和一间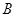 型板房所需板材及能安置的人数如下表所示:
型板房所需板材及能安置的人数如下表所示:
| 板房型号 |
甲种板材 |
乙种板材 |
安置人数 |
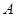 型板房 型板房 |
54  |
26  |
5 |
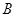 型板房 型板房 |
78  |
41  |
8 |
问:这400间板房最多能安置多少灾民?