已知函数 与
与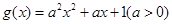
(1)设直线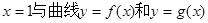 分别相交于点
分别相交于点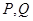 ,且曲线
,且曲线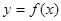 和
和 在点
在点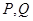 处的切线平行,求实数
处的切线平行,求实数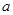 的值;
的值;
(2)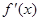 为
为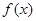 的导函数,若对于任意的
的导函数,若对于任意的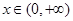 ,
,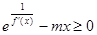 恒成立,求实数
恒成立,求实数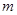 的最大值;
的最大值;
(3)在(2)的条件下且当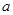 取
取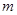 最大值的
最大值的 倍时,当
倍时,当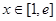 时,若函数
时,若函数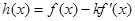 的最小值恰为
的最小值恰为 的最小值,求实数
的最小值,求实数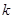 的值
的值
已知椭圆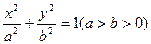 的离心率为
的离心率为 ,长轴长为
,长轴长为 ,直线
,直线 交椭圆于不同的两点A、B。
交椭圆于不同的两点A、B。
(1)求椭圆的方程;
(2)求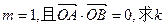 的值(O点为坐标原点);
的值(O点为坐标原点);
(3)若坐标原点O到直线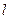 的距离为
的距离为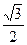 ,求
,求 面积的最大值。
面积的最大值。
在数列 中,
中,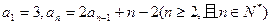
(1)求 的值;
的值;
(2)证明:数列 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式;
(3)求数列 。
。
如图,已知直三棱柱ABC—A1B1C1, 。E、F分别是棱CC1、AB中点。
。E、F分别是棱CC1、AB中点。
(1)求证: ;
;
(2)求四棱锥A—ECBB1的体积;
(3)判断直线CF和平面AEB1的位置关系,并加
以证明。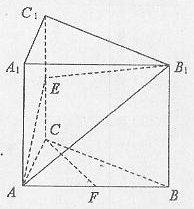
为援助汶川灾后重建,对某项工程进行竞标,共有6家企业参与竞标,其中A企业来自辽宁省,B、C两家企业来自福建省,D、E、F三家企业来自河南省,此项工程需要两家企业联合施工,假设每家企业中标的概率相同。
(1)企业E中标的概率是多少?
(2)在中标的企业中,至少有一家来自河南省的概率是多少?
在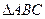 中,角A、B、C所对的边分虽为
中,角A、B、C所对的边分虽为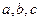 ,且
,且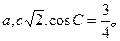
(1)求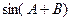 的值;
的值;
(2)求 的值;
的值;
(3)求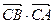 的值。
的值。