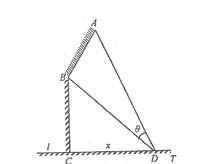
如图,某机场建在一个海湾的半岛上,飞机跑道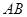 的长为4.5
的长为4.5 ,且跑道所在的直线与海岸线
,且跑道所在的直线与海岸线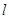 的夹角为
的夹角为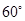 (海岸线可以看作是直线),跑道上离海岸线距离最近的点
(海岸线可以看作是直线),跑道上离海岸线距离最近的点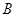 到海岸线的距离
到海岸线的距离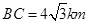 .
. 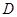 为海湾一侧海岸线
为海湾一侧海岸线 上的一点,设
上的一点,设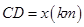 ,点
,点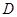 对跑道
对跑道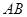 的视角为
的视角为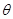 .
.
(1) 将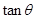 表示为
表示为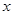 的函数;
的函数;
(2)已知常数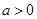 ,对于任意的
,对于任意的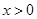 ,
, 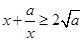 ,等号成立当
,等号成立当
且仅当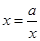 ,求点
,求点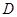 相对于垂足
相对于垂足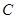 的位置,使
的位置,使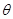 取得最大值.
取得最大值.
观察以下各等式: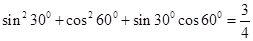

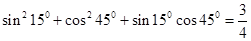 ,
,
分析上述各式的共同特点,猜想出反映一般规律的等式,并对等式的正确性作出证明。
某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,在将两组工人的日平均生产件数分成5组: ,
, ,
, ,
, ,
,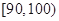 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.
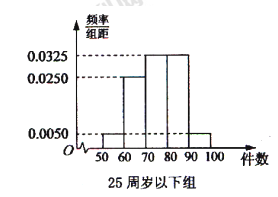

(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的频率.
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成 的列联表,并判断是否有
的列联表,并判断是否有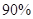 的把握认为“生产能手与工人所在的年龄组有关”?
的把握认为“生产能手与工人所在的年龄组有关”?
附表: 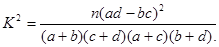
从某居民区随机抽取10个家庭,获得第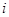 个家庭的月收入
个家庭的月收入 (单位:千元)与月储蓄
(单位:千元)与月储蓄 (单位:千元)的数据资料,算得
(单位:千元)的数据资料,算得 ,
, ,
, ,
, .
.
(1)求家庭的月储蓄 对月收入
对月收入 的线性回归方程
的线性回归方程 ;
;
(2)判断变量 与
与 之间是正相关还是负相关;
之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
其中 ,
,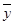 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为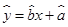
附:线性回归方程 中,
中,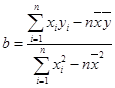 ,
, ,
,
设过原点 的直线与圆
的直线与圆 :
: 的一个交点为
的一个交点为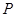 ,点
,点 为线段
为线段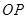 的中点。
的中点。
(1)求圆 的极坐标方程;
的极坐标方程;
(2)求点 轨迹的极坐标方程,并说明它是什么曲线.
轨迹的极坐标方程,并说明它是什么曲线.
已知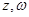 为复数,
为复数, 为纯虚数,
为纯虚数,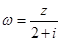 ,且
,且 ,求复数
,求复数 .
.