已知Sn是数列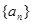
的前n项和，且
（Ⅰ）求数列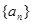的通项公式；
（Ⅱ）设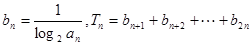
，是否存在最大的正整数k，使得对于任意的正整数n，有
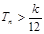恒成立？若存在，求出k的值；若不存在，说明理由.
在△ABC中，a.b.c分别为内角A.B.C所对的边，且满足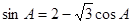
（1）求角A的大小
（2）现给出三个条件：①a=2.②B=45°③C=
试从中选出两个可以确定△ABC的条件写出你的
选择，并以此为依据求△ABC的面积（只需写出一个选定方案即可，选多种方案以第一种方案记
分）
命题P：实数x满足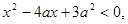
其中a<0，命题q：实数x满足
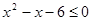或
且
是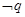
的必要不充分条件，求a的取值范围
已知函数
的最大值是1，其图象经过点M
（1）求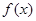
的解析式（2）已知
且
求
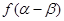的值。
已知函数f（x）=lnx，g（x）=
（a≠0）
（1）若b=2,且h（x）=f（x）-g（x）在定义域上不单调，求a的取值范围；
（2）若a=1,b=-2设f（x）的图象C1与g（x）的图象C2交于点P、Q，过线段PQ的中点作x轴的垂线分别交C1，C2于点M、N，M、N的横坐标是m，求证：f＇（m）＜g＇（m）。
某家庭为小孩买教育保险，小孩在出生的第一年父母就交纳保险金，数目为a1，以后每年交纳的数目均比上一年增加d（d＞0），因此，历年所交纳的保险金数目为a1,a2,…是一个公差为d的等差数列，与此同时保险公司给予优惠的利息政策，不仅采用固定利率，而且计算复利，这就是说，如果固定利率为r（ｒ＞0），那么，在第n年末，第一年所交纳的保险金就变为a1（1+r）n-1，第二年所交纳的保险金就变为a2（1+r）n-2,…，以Tn表示到第n年末所累计的保险金总额。
（1）写出Tn与Tn+1的递推关系（n≥1）；
（2）若a1=1,d=0.1，求｛Tn｝的通项公式。（用r表示）