（本小题满分12分）
2012年4月15日，央视《每周质量报告》曝光某省一些厂商用生石灰处理皮革废料，熬制成工业明胶，卖给一些药用胶囊生产企业，由于皮革在工业加工时，要使用含铬的鞣制剂，因此这样制成的胶囊，往往重金属铬超标，严重危害服用者的身体健康。该事件报道后，某市药监局立即成立调查组，要求所有的药用胶囊在进入市场前必须进行两轮检测，只有两轮都合格才能进行销售，否则不能销售，两轮检测是否合格相互没有影响。
（1）某药用胶囊共生产3个不同批次，经检测发现有2个批次为合格，另1个批次为不合格，现随机抽取该药用胶囊5件，求恰有2件不能销售的概率；
（2）若对某药用胶囊的3个不同批次分别进行两轮检测，药品合格的概率如下表：
| |
第1批次 |
第2批次 |
第3批次 |
| 第一轮检测 |
 |
 |
 |
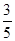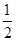| 第二轮检测 |
 |
 |
|
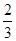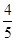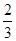记该药用胶囊能通过检测进行销售的批次数为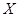
，求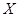的分布列及数学期望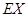
一直线过点P(-5,-4),且与两坐标轴围成的三角形面积为5,求此直线方程.
条直线在两轴上的截距相等,且与两轴围成的三角形的周长为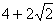
,求此直线的方程.
(1)求经过点(1,1),且与直线y=2x+7平行的直线的方程;
(2)求经过点(0,2),且与直线y=-3x-5平行的直线的方程;
(3)求经过点(-1,1),且与直线y=-2x+7垂直的直线的方程;
(4)求经过点(-2,-2),且与直线y=3x-5垂直的直线的方程.
求过点A(5,2),且在坐标轴上截距互为相反数的直线l的方程.
根据下列条件,写出直线的方程.
(1)斜率是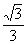
,经过点A(8,-2);
(2)经过点B(-2,0),且与x轴垂直;
(3)斜率为-4,在y轴上的截距为7;
(4)经过点A(-1,8),B(4,-2);
(5)在y轴上的截距是2,且与x轴平行;
(6)在x轴,y轴上的截距分别是4,-3.