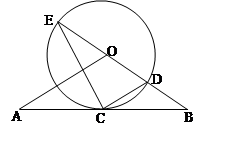
如图,直线 经过⊙
经过⊙ 上的点
上的点 ,并且
,并且 ⊙
⊙ 交直线
交直线 于
于 ,
, ,连接
,连接 .
.
(I)求证:直线 是⊙
是⊙ 的切线;
的切线;
(II)若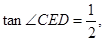 ⊙
⊙ 的半径为
的半径为 ,求
,求 的长.
的长.
(本小题满分13分)已知椭圆 过点
过点 ,且与抛物线
,且与抛物线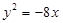 有一个公共的焦点.
有一个公共的焦点.
(Ⅰ)求椭圆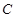 方程;
方程;
(Ⅱ)过椭圆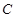 的右焦点
的右焦点 且斜率为
且斜率为 的直线
的直线 与椭圆
与椭圆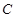 交于
交于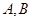 两点,求弦
两点,求弦 的长;
的长;
(Ⅲ)以第(Ⅱ)题中的 为边作一个等边三角形
为边作一个等边三角形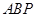 ,求点
,求点 的坐标.
的坐标.
(本小题满分12分)等差数列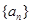 中,
中, ,其前
,其前 项和为
项和为 .等比数列
.等比数列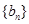 的各项均为正数,
的各项均为正数,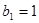 ,且
,且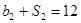 ,
,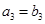 .
.
(Ⅰ)求数列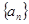 与
与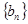 的通项公式;
的通项公式;
(Ⅱ)求数列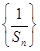 的前
的前 项和
项和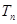 .
.
(本小题满分12分)如图,将边长为2,有一个锐角为60°的菱形 ,沿着较短的对角线
,沿着较短的对角线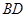 对折,使得
对折,使得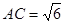 ,
, 为
为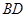 的中点.若P为AC上的点,且满足
的中点.若P为AC上的点,且满足 .
.
(Ⅰ)求证: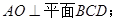
(Ⅱ)求三棱锥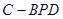 的体积;
的体积;
(本小题满分12分)已知向量m=(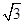 sinωx,cosωx),n=(cosωx,-cosωx),若函数f(x)=m·n的图象关于直线
sinωx,cosωx),n=(cosωx,-cosωx),若函数f(x)=m·n的图象关于直线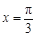 对称,其中ω取所有可能值中的最小正数值.
对称,其中ω取所有可能值中的最小正数值.
(Ⅰ)求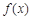 的周期和单调递增区间;
的周期和单调递增区间;
(Ⅱ)△ABC中,如果f( )=
)= ,b=4
,b=4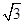 ,且asinA-bsinB=sinC(c-
,且asinA-bsinB=sinC(c-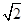 b),求△ABC的面积.
b),求△ABC的面积.
(本小题满分12分)一次数学测验,某班50名同学的成绩全部介于90分到140分之间.将成绩结果按如下方式分成五组:第一组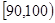 ,第二组
,第二组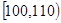 ,……,第五组
,……,第五组 .按上述分组方法得到的频率分布直方图如图所示.
.按上述分组方法得到的频率分布直方图如图所示.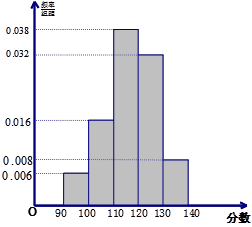
(Ⅰ)若成绩大于或等于100分且小于120分认为是良好的,求该校参赛学生在这次数学联赛中成绩良好的人数;
(Ⅱ)若从第一、五组中随机取出两个同学的成绩,求这两个成绩差的绝对值大于30分的概率.