某高中三年级有一个实验班和一个对比班，各有50名同学．根据这两个班市二模考试的数学科目成绩（规定考试成绩在[120，150]内为优秀），统计结果如下：
实验班数学成绩的频数分布表：
对比班数学成绩的频数分布表：
（Ⅰ）分别求这两个班数学成绩的优秀率；若采用分层抽样从实验班中抽取15位同学的数学试卷，进行试卷分析，则从该班数学成绩为优秀的试卷中应抽取多少份?
（Ⅱ）统计学中常用M值作为衡量总体水平的一种指标，已知M与分数t的关系式为：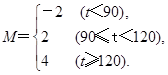
分别求这两个班学生数学成绩的M总值，并据此对这两个班数学成绩总体水平作一简单评价．
（本小题满分12分）
如图，在四棱锥P—ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F．
⑴证明PA//平面EDB；
⑵证明PB⊥平面EFD；
⑶求二面角C—PB—D的大小．
已知函数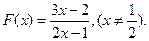
（1）求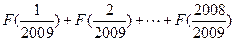
的值；
（2）已知数列
,求数列
的通项公式；
（3）求证: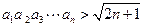
．
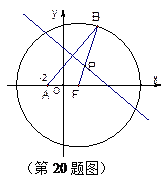
已知定点A（－2，0），动点B是圆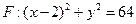
（F为圆心）上一点，线段AB的垂直平分线交BF于P．
（1）求动点P的轨迹方程；
（2）是否存在过点E（0，－4）的直线l交P点的轨迹于点R，T，且满足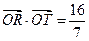
（O为原点）．若存在，求直线l的方程；若不存在，请说明理由．
已知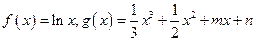
，直线
与函数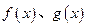
的图象都相切于点
．
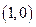（1）求直线的方程及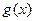
的解析式；
（2）若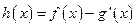
（其中
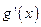是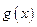
的导函数），求函数
的值域．
某种家用电器每台的销售利润与该电器的无故障使用时间T (单位:年)有关．若T≤1，则销售利润为0元；若1＜T≤3，则销售利润为100元；若T＞3，则销售利润为200元．设每台该种电器的无故障使用时间T≤1，1＜T≤3及T＞3这三种情况发生的概率分别为p1，p2，p3，又知p1，p2是方程
的两个根，且p2=p3．
（1）求p1，p2，p3的值；
（2）记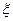
表示销售两台这种家用电器的销售利润总和，求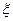的期望．