如图，在平面直角坐标系中，锐角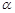
、
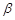的终边分别与单位圆交于
，
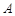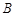两点．
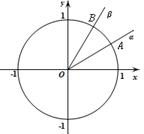
（Ⅰ）如果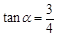
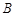，点的横坐标为
，求
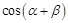的值；
（Ⅱ）若角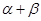
的终边与单位圆交于C点，设角
、
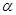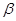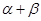、的正弦线分别为MA、NB、PC，求证：线段MA、NB、PC能构成一个三角形；
（III）探究第（Ⅱ）小题中的三角形的外接圆面积是否为定值？若是，求出该定值；若不是，请说明理由.
已知圆的方程是x2+y2=2,直线y=x+b,当b为何值时,圆与直线有两个公共点?
一艘轮船沿直线返回港口的途中,接到气象台的台风预报,台风中心位于轮船正西70 km处,受影响的范围是半径为30 km的圆形区域,已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?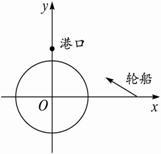 
已知圆C1：x2+y2+2x+8y-8=0，圆C2：x2+y2-4x-4y-2=0，试判断圆C1与圆C2的关系.
求圆心在直线x+y=0上，且过两圆x2+y2-2x+10y-24=0，x2+y2+2x+2y-8=0的交点的圆的方程.
已知圆C1:x2+y2-2mx+4y+m2-5="0," 圆C2: x2+y2+2x-2my+m2-3=0,当m为何值时,圆C1与圆C2相切?