(本小题满分8分)
已知函数 ,且
,且 .
.
(1)求实数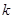 的值
的值
(2)判断并证明函数在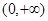 上的单调性;
上的单调性;
已知函数
(1)当
时,求不等式
的解集;
(2)若
的解集包含
,求
的取值范围.
已知曲线 的参数方程是 ,以坐标原点为极点, 轴的正半轴为极轴建立坐标系,曲线 的坐标系方程是 ,正方形 的顶点都在 上,且 依逆时针次序排列,点 的极坐标为
(1)求点
的直角坐标;
(2)设
为
上任意一点,求
的取值范围.
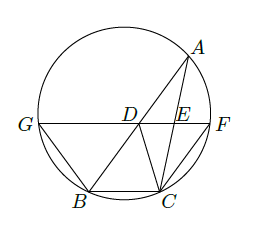
如图,
分别为
边
的中点,直线
交
的外接圆于
两点,若
,证明:
(1)
;
(2)
已知函数
满足满足
;
(1)求
的解析式及单调区间;
(2)若
,求
的最大值.
设抛物线
的焦点为
,准线为
,
,已知以
为圆心,
为半径的圆
交
于
两点;
(1)若
,
的面积为
;求
的值及圆
的方程;
(2)若
三点在同一直线
上,直线
与
平行,且
与
只有一个公共点,求坐标原点到
距离的比值.