如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由. 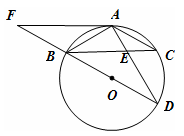
(1)解方程: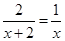 ;
;
(2)解不等式组: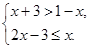
计算:
(1) ;
;
(2)
在直角坐标系 中,已知点P是反比例函数
中,已知点P是反比例函数 (
( >0)图象上一个动点,以P为圆心的圆始终与
>0)图象上一个动点,以P为圆心的圆始终与 轴相切,设切点为A.
轴相切,设切点为A.

(1)如图1,⊙P运动到与 轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
(2)如图2,⊙P运动到与 轴相交,设交点为B,C.当四边形ABCP是菱形时:
轴相交,设交点为B,C.当四边形ABCP是菱形时:
①求出点A,B,C的坐标.
②在过A,B,C三点的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的 .若存在,试求出所有满足条件的M点的坐标,若不存在,试说明理由.
.若存在,试求出所有满足条件的M点的坐标,若不存在,试说明理由.
【问题引入】
几个人拎着水桶在一个水龙头前面排队打水,水桶有大有小.他们该怎样排队才能使得总的排队时间最短?
假设只有两个人时,设大桶接满水需要T分钟,小桶接满水需要t分钟(显然T>t),若拎着大桶者在拎小桶者之前,则拎大桶者可直接接水,只需等候T分钟,拎小桶者一共等候了(T+t)分钟,两人一共等候了(2T+t)分钟;反之,若拎小桶者在拎大桶者之前,容易求出两人接满水等候(T+2t)分钟。可见,要使总的排队时间最短。拎小桶者应排在拎大桶者前面。这样,我们可以猜测,几个人拎着水桶在一个水龙头前面排队打水,要使总的排队时间最短,需将他们按水桶从小到大排队.
规律总结:
事实上,只要不按照从小到大的顺序排队,就至少有紧挨着的两个人拎大桶者排在拎小桶者之前,仍设大桶接满水需要T分钟,小桶接满水需t分钟,并设拎大桶者开始接水时已经等候了m分钟,这样拎大桶者接满水一共等候了(m+T)分钟,拎小桶者接满水一共等候了(m+T+t)分钟,两人共等候了(2m+2T+t)分钟,在其他人位置不变的前提下,让这两个人交换位置,即局部调整这两个人的位置,同样可以计算两个人接满水共等候了 __ ___分钟,共节省了 _________分钟,而其他人的等候时间未变。这说明只要存在有紧挨着的两个人是拎大桶者在拎小桶者前,都可以这样局部调整,从而使得总等候时间减少。这样经过一系列调整之后,整个队伍都是从小到大排列,就达到最优状态,总的排队时间就最短.
【方法探究】
一般地,对某些涉及多个可变对象的数学问题,先对其少数对象进行调整,其他对象暂时保持不变,从而化难为易,取得问题的局部解决.经过若干次这种局部的调整,不断缩小范围,逐步逼近目标,最终使问题得到解决,这种数学思想方法就叫做局部调整法.
【实践应用1】
如图1,在锐角△ABC中,AB=4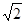 ,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?
,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?
解析:(1)先假定N为定点,调整M到合适位置,使BM+MN有最小值(相对的).
容易想到,在AC上作AN′=AN(即作点N关于AD的对称点N′),连接BN′交AD于M,则M点是使BM+MN有相对最小值的点.(如图2,M点确定方法找到)
(2)再考虑点N的位置,使BM+MN最终达到最小值.
可以理解,BM+MN = BM+MN′,所以要使BM+MN′有最小值,只需使,此时BM+MN的最小值为.
【实践应用2】
如图,把边长是3的正方形等分成9个小正方形,在有阴影的两个小正方形内(包括边界)分别任取点P、R,与已知格点Q(每个小正方形的顶点叫做格点)构成三角形,求△PQR的最大面积,并在图2中画出面积最大时的△PQR的图形.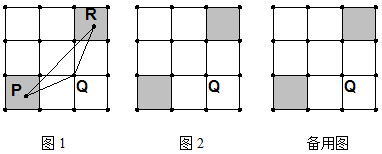
(8分)如图,四边形 是平行四边形,点
是平行四边形,点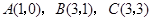 .反比例函数
.反比例函数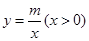 的图象经过点
的图象经过点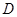 ,点
,点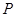 是一次函数
是一次函数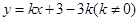 的图象与该反比例函数图象的一个公共点.
的图象与该反比例函数图象的一个公共点.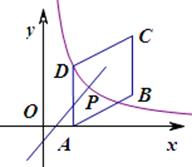
(1)求反比例函数的解析式;
(2)通过计算,说明一次函数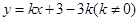 的图象一定过点
的图象一定过点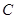 ;
;
(3)对于一次函数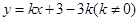 ,当
,当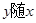 的增大而增大时,确定点
的增大而增大时,确定点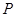 横坐标的取值范围(不写过程,直接写出结果).
横坐标的取值范围(不写过程,直接写出结果).