为了迎接党的十八大的召开，某校组织了以“党在我心中”为主题的征文比赛，每位学生只能参加一次比赛，比赛成绩分A、B、C、D四个等级，随机抽取该校部分学生的征文比赛成绩进行分析，并绘制了如下的统计图表：
| 成绩等级 |
A |
B |
C |
D |
| 人数 |
60 |
x |
y |
10 |
| 占抽查学生总数的百分比 |
30% |
50% |
15% |
m |
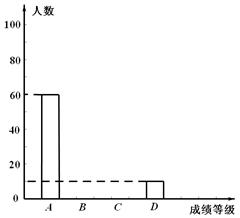
根据表中的信息，解决下列问题：
（1）本次抽查的学生共有 ▲ 名；
（2）表中x、y和m所表示的数分别为x= ▲ ，y= ▲ ，m= ▲ ；
（3）补全条形统计图。
阅读并解答下列问题：我们熟悉两个乘法公式：①（
+b）2=2+2b+b2;②(-b)2=2-2b+b2.现将这两个公式变形，可得到一个新的公式③：b=(
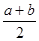)2-(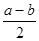
)2, 这个公式形似平方差公式，我们不妨称之为广义的平立差公式。灵活、恰当地运用公式③将会使一些数学问题迎刃而解。
例如：因式分解：（b-1）2+(+b-2)( +b-2b)
解：原式=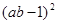
+
-
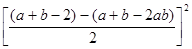
=(b-1)2+(+b-b-1)2-(b-1)2=(-1)(b-1)2=（-1）2(b-1)2你能利用公式（或其他方法）解决下列问题吗？
已知各实数，b，c满足b=c2+9且=6-b，求证：="b"
一列火车自A城驶往B城,沿途有n个车站(包括起点站A和终点站B),该列火车挂有一节邮政车厢,运行时需要在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该站的邮包一个,还要装上该站发往下面行程中每个车站的邮包一个。例如,当列车停靠在第x 个车站时,邮政车厢上需要卸下已经通过的(x-1)个车站发给该站的邮包共(x-1)个,还要装上下面行程中要停靠的(n-x)个车站的邮包共(n-x)个。
(1)根据题意,完成下表:
| 车站序号 |
在第x车站启程时邮政车厢邮包总数 |
| 1 |
n-1 |
| 2 |
(n-1)-1+(n-2)=2(n-2) |
| 3 |
2(n-2)-2+(n-3)=3(n-3) |
| 4 |
|
| 5 |
|
| … |
…… |
| n |
(2)根据上表,写出列车在第x车站启程时,邮政车厢上共有邮包的个数y(用x、
n表示)。
(3)当n=18时,列车在第几个车站启程时邮政车厢上邮包的个数最多？
如图.AD、AH分别是△ABC（其中AB＞AC）的角平分线、高线，M点是AD的中点，△MDH的外接圆交CM于E，求证∠AEB=90°。
抛物线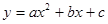
的图像于x轴交于点M
，N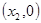
，且经过点A（0，1），其中
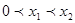，过点A的直线
交x轴于C点，与抛物线交于点B（异于A点），满足△CAN是等腰直角三角形，且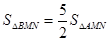
，求解析式.
已知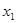
、
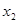是关于x的一元二次方程
的两个实数根，使得
成立，求其实数
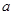的可能值。