(本小题满分12分)
如图所示, 四棱锥P-ABCD的底面是边长为1的正方形,PA^CD,PA = 1, PD=,E为PD上一点,PE = 2ED.

(Ⅰ)求证:PA^平面ABCD;
(Ⅱ)求二面角D-AC-E的余弦值;
(Ⅲ)在侧棱PC上是否存在一点F,使得BF // 平面AEC?若存在,指出F点的位置,并证明;若不存在,说明理由.
(本题满分14分袋中有大小相同的红、黄两种颜色的球各 个,从中任取
个,从中任取 只,有放回地抽取
只,有放回地抽取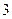 次
次 求: ①
求: ①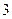 只全是红球的概率; ②
只全是红球的概率; ②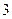 只颜色全相同的概率;③
只颜色全相同的概率;③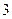 只颜色不全相同的概率
只颜色不全相同的概率
在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按照5天一组分组统计,绘制了频率分布直方图(如图所示).已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列各题.
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪一组获奖率较高?
设有关于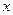 的一元二次方程
的一元二次方程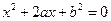 。
。
(Ⅰ)若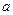 是从
是从 四个数中任取的一个数,
四个数中任取的一个数,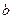 是从
是从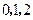 三个数中任取的一个数,求上述方程有实根的概率.
三个数中任取的一个数,求上述方程有实根的概率.
(Ⅱ)若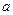 是从区间
是从区间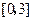 任取的一个数,
任取的一个数,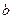 是从区间
是从区间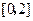 任取的一个数,
任取的一个数,
求上述方程有实根的概率
先后随机投掷2枚正方体骰子,其中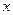 表示第
表示第 枚骰子出现的点数,
枚骰子出现的点数,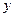 表示第
表示第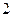 枚骰子出现的点数。设点P的坐标为
枚骰子出现的点数。设点P的坐标为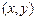 。
。
(Ⅰ)求点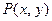 在直线
在直线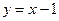 上的概率;
上的概率;
(Ⅱ)求点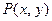 满足
满足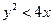 的概率。
的概率。
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(Ⅰ)用茎叶图表示这两组数据;若将频率视为概率,对甲学生在培训后参加的一次数学竞赛成绩进行预测,求甲的成绩高于80分的概率;
(Ⅱ)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由