证明函数
在（－∞，0）上是增函数。
集合P=｛x︱x2-2x-3=0｝，S=｛x︱ax+2=0｝，SÍP，求a的值。
如图，有一壁画，最高点A处离地面4m，最低点B处离地面2m，若从离地高1.5m的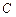
处观赏它，则离墙多远时，视角
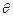最大？
选做题（本小题满分10分。请考生三两题中任选一题做答，如果多做，
则按所做的第一题记分）
选修4－1：几何证明选讲
如图，圆O的直径AB=10，弦DE⊥AB于点H，BH=2。1）求DE的长；
（2）延长ED到P，过P作圆O的切线，
切点为C，若ＰＣ＝２
，求ＰＤ的长。
选修4－5：不等式选讲
（Ⅰ）若
与2的大小,不用说明理由;
（Ⅱ）设m是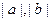
和1中最大的一个,当
已知函数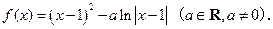
（1）当
时，求函数
的单调区间；
（2）求函数在区间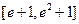
上的最小值．
