分别求出经过点P(3,4)且满足下列条件的直线方程,并画出图形.
①斜率k=2;②与x轴平行;③与x轴垂直.
如图,已知点A(2,5)与点B(4,-7),试在y轴上求一点P,使得|PA|+|PB|的值为最小.
已知点M(2,2)和N(5,-2),点P在x轴上,且∠MPN为直角,求P点坐标.
判断下列各小题中的每对直线是否垂直:
①l1的斜率为 ,l2经过点A(1,1),B(0,
,l2经过点A(1,1),B(0,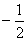 );
);
②l1的倾斜角为45°,l2经过点P(-2,-1),Q(3,-6);
③l1经过点M(1,0),N(4,-5),l2经过点R(-6,0),S(-1,3)
已知l1经过A(-3,3),B(-8,6),l2经过M( ,6),N(
,6),N(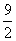 ,-3,求证:l1∥l2.
,-3,求证:l1∥l2.