某校开展了以“人生观、价值观”为主题的班队活动,活动结束后,九(2)班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图.
(1)该班学生选择“互助”观点的有 人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是 度;
(2)如果该校有1500名九年级学生,利用样本估计选择“感恩”观点的九年级学生约有__420____人.
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率.(用树状图或列表法分析解答)
已知:抛物线y=-x2+2x+m-2交y轴于点A(0,2m-7).与直线
y=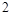 x交于点B、C(B在右、C在左).
x交于点B、C(B在右、C在左).求抛物线的解析式
设抛物线的顶点为E,在抛物线的对称轴上是否存在一点F,使得
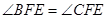 ,若存在,求出点F的坐标,若不存在,说明理由
,若存在,求出点F的坐标,若不存在,说明理由射线OC上有两个动点P、Q同时从原点出发,分别以每秒
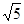 个单位长度、每秒2
个单位长度、每秒2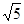 个单位长度的速度沿射线OC运动,以PQ为斜边在直线BC的上方作直角三角形PMQ(直角边分别平行于坐标轴),设运动时间为t秒,若△PMQ与抛物线y=-x2+2x+m-2有公共点,求t的取值范围.
个单位长度的速度沿射线OC运动,以PQ为斜边在直线BC的上方作直角三角形PMQ(直角边分别平行于坐标轴),设运动时间为t秒,若△PMQ与抛物线y=-x2+2x+m-2有公共点,求t的取值范围.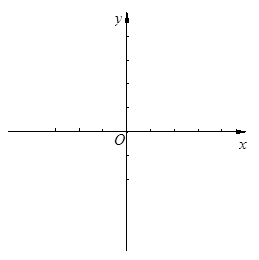
在△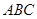 中,
中,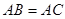 ,
,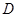 是底边
是底边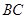 上一点,
上一点,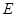 是线段
是线段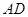 上一点,且
上一点,且
∠ .
.如图1,若∠
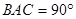 ,猜想
,猜想 与
与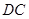 的数量关系为;
的数量关系为;如图2,若∠
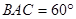 ,猜想
,猜想 与
与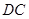 的数量关系,并证明你的结论;
的数量关系,并证明你的结论;若∠
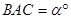 ,请直接写出
,请直接写出 与
与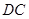 的数量关系.
的数量关系.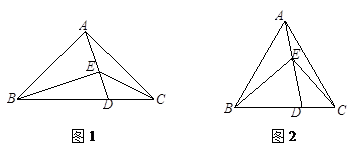
已知:直线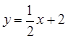 分别与 x轴、y轴交于点A、点B,点P(
分别与 x轴、y轴交于点A、点B,点P(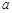 ,b)在直线AB 上,点P关于
,b)在直线AB 上,点P关于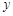 轴的对称点P′ 在反比例函数
轴的对称点P′ 在反比例函数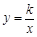 图象上.
图象上.当a=1时,求反比例函数
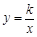 的解析式
的解析式设直线AB与线段P'O的交点为C.当P'C =2CO时,求b的值;
过点A作AD//y轴交反比例函数图象于点D,若AD=
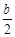 ,求△P’DO的面积.
,求△P’DO的面积. 
小阳遇到这样一个问题:如图(1),O为等边△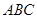 内部一点,且
内部一点,且 ,求
,求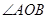 的度数.
的度数.
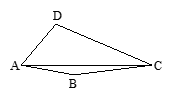
|
 绕点A逆时针旋转60°,使点C与点B重合,得到△
绕点A逆时针旋转60°,使点C与点B重合,得到△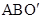 ,连结
,连结 . 则△
. 则△ 是等边三角形,故
是等边三角形,故 ,至此,通过旋转将线段OA、OB、OC转移到同一个三角形
,至此,通过旋转将线段OA、OB、OC转移到同一个三角形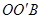 中.
中.
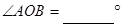 .
.
已知:如图,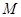 是⊙
是⊙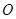 的直径
的直径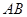 上任意一点,过点
上任意一点,过点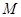 作
作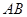 的垂线
的垂线 ,
,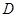 是
是 的延长线上一点,联结
的延长线上一点,联结 交⊙
交⊙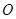 于点
于点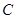 ,且
,且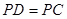 .
.
判断直线
 与⊙
与⊙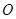 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;若
 ,
,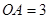 ,过点A作
,过点A作 的平行线
的平行线 交⊙
交⊙ 于点
于点 .求弦
.求弦 的长.
的长.