椭圆E的中心在坐标原点O,焦点在x轴上,离心率为.点P(1,)、A、B在椭圆E上,且+=m(m∈R).
(1)求椭圆E的方程及直线AB的斜率;
(2)当m=-3时,证明原点O是△PAB的重心,并求直线AB的方程.
已知函数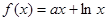 ,其中
,其中 为常数,设
为常数,设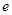 为自然对数的底数.
为自然对数的底数.
(1)若 在区间
在区间 上的最大值为-3,求
上的最大值为-3,求 的值;
的值;
(2)当 时,试推断方程
时,试推断方程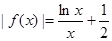 是否有实数解.
是否有实数解.
数列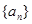 中,
中,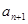 是函数
是函数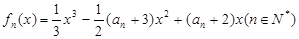 的极小值点,且
的极小值点,且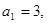

(1)求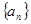 的通项公式;
的通项公式;
(2)记 为数列
为数列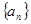 的前
的前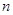 项和,试比较
项和,试比较 与
与 的大小关系.
的大小关系.
设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的五个盒子,现将这五个球放入5个盒子内. (答题要求:先列式,后计算)
(1)恰有一个盒子空着,共有多少种投放方法?
(2)每个盒子内投放一球,并且至少有两个球的编号与盒子编号是相同的,有多少种投放方法?
已知函数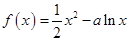 (
( )
)
(1)若函数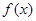 的图象在
的图象在 处的切线方程为
处的切线方程为 ,求
,求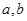 的值;
的值;
(2)若函数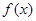 在
在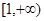 为增函数,求
为增函数,求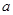 的取值范围.
的取值范围.
已知抛物线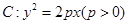 上横坐标为
上横坐标为 的点
的点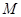 到焦点
到焦点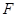 的距离为
的距离为 .
.
(1)求抛物线的方程;
(2)若斜率为 的直线
的直线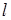 与抛物线
与抛物线 交于
交于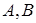 两点,且点
两点,且点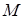 在直线
在直线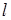 的右上方,求证:△
的右上方,求证:△ 的内心在直线
的内心在直线 上.
上.