(本小题满分10分)选修4—5;不等式选讲.
设不等式 的解集是
的解集是 ,
,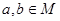 .
.
(I)试比较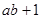 与
与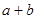 的大小;
的大小;
(II)设 表示数集
表示数集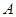 的最大数.
的最大数.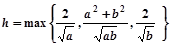 ,求证:
,求证: .
.
如图1,在直角梯形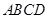 中,
中,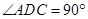 ,
,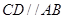 ,
,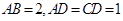 .将
.将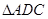 沿
沿 折起,使平面
折起,使平面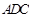
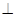 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.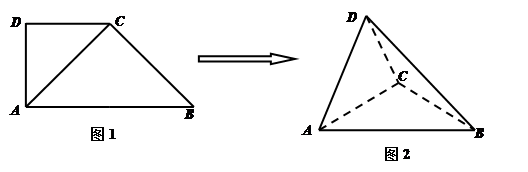
(1)求证: 平面
平面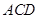 ;(2)求几何体
;(2)求几何体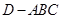 的体积.
的体积.
一个盒子中装有标号为1,2,3,4的4张标签,随机地选取两张标签,根据下列条件求两张标签上的数字为相邻整数的概率:
(1) 标签的选取是无放回的; (2) 标签的选取是有放回的.
(1)求 的定义域;(2)设
的定义域;(2)设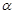 是第二象限的角,且tan
是第二象限的角,且tan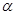 =
=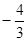 ,求
,求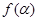 的值.
的值.
在数列{an}中,a1=1,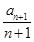 =
=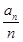 +
+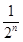 .
.
(1)设bn=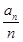 ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(2)求数列{an}的前n项和Sn.
已知△ABC的周长为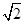 +1,且sin A+sin B=
+1,且sin A+sin B=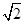 sin C.
sin C.
(1)求边AB的长;
(2)若△ABC的面积为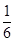 sin C,求角C的度数.
sin C,求角C的度数.