(本小题满分12分)某赛季,甲、乙两名篮球运动员都参加了10场比赛,比赛得分情况记录如下(单位:分):
甲:37,21,31,20,29,19,32,23,25,33
乙:10,30,47,27,46,14,26,10,44,46
(Ⅰ)根据得分情况记录,作出两名篮球运动员得分的茎叶图,并根据茎叶图,对甲、乙两运动员得分作比较,写出两个统计结论;
(Ⅱ)设甲篮球运动员10场比赛得分平均值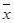 ,将10场比赛得分
,将10场比赛得分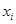 依次输入如图所示的程序框图进行运算,问输出的
依次输入如图所示的程序框图进行运算,问输出的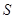 大小为多少?并说明
大小为多少?并说明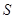 的统计学意义;
的统计学意义;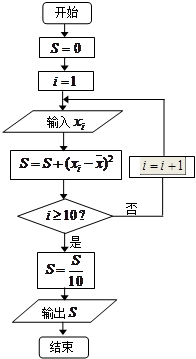
(Ⅲ)如果从甲、乙两位运动员的10场得分中,各随机抽取一场不小于30分的得分,求甲的得分大于乙的得分的概率.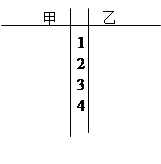
已知向量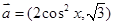 ,
, ,函数
,函数 .
.
(1)求函数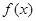 的最小正周期;
的最小正周期;
(2)若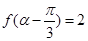 ,
,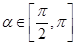 ,求
,求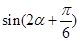 的值.
的值.
对于函数 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.
(1)已知函数
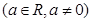 ,试判断
,试判断 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)若 为定义域
为定义域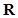 上的“局部奇函数”,求实数m的取值范围.
上的“局部奇函数”,求实数m的取值范围.
已知椭圆 (
( >
> >0)的离心率
>0)的离心率 ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.
(1)求椭圆的方程;
(2)设直线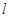 与椭圆相交于不同的两点
与椭圆相交于不同的两点 ,已知点
,已知点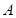 的坐标为(
的坐标为(  ,0),点
,0),点 (0,
(0,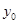 )在线段
)在线段 的垂直平分线上,且
的垂直平分线上,且 ,求
,求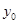 的值.
的值.
在数列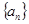 和
和 中,已知
中,已知 .
.
(1)求数列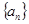 和
和 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列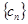 的前n项和
的前n项和 .
.
已知四棱锥 的底面
的底面 是等腰梯形,
是等腰梯形, 且
且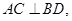


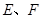 分别是
分别是 的中点.
的中点.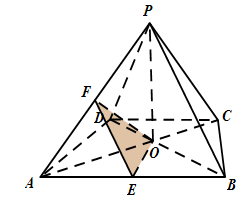
(1)求证: ;
;
(2)求二面角 的余弦值.
的余弦值.