已知: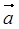 、
、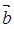 、
、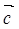 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中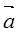 =(1,2)
=(1,2)
⑴若| |
|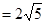 ,且
,且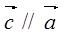 ,求
,求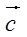 的坐标;
的坐标;
⑵若|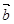 |=
|=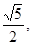 且
且 与
与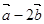 垂直,求
垂直,求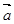 与
与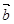 的夹角θ.
的夹角θ.
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于D.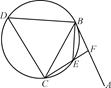
(1)证明:DB=DC;
(2)设圆的半径为1,BC=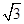 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
如图,AB和BC分别与圆O相切于点D、C,AC经过圆心O,且BC=2OC.求证:AC=2AD.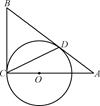
如图,在△ABC中,∠C=90°,∠A=60°,AB=20,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,求DE的长.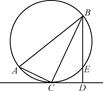
如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2,求BC的值.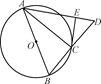
如图,PA切圆O于点A,割线PBC交圆O于点B、C,∠APC的角平分线分别与AB、AC相交于点D、E,求证:
(1)AD=AE;
(2)AD2=DB·EC.