（（本题14分）定义：若函数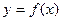
在某一区间D上任取两个实数
、
，且
，都有
，则称函数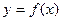在区间D上具有性质L。
（1）写出一个在其定义域上具有性质L的对数函数（不要求证明）。
（2）对于函数
，判断其在区间
上是否具有性质L？并用所给定义证明你的结论。
（3）若函数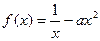
在区间（0，1）上具有性质L，求实数
的取值范围。
在正方体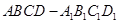
中，M、N、P分别是
的中点，求证：平面MNP//平面
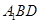
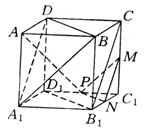
如图在三棱锥S
中
，
，
，
，
.
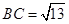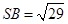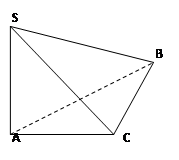
（1）证明
。
（2）求侧面
与底面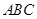
所成二面角的大小。
（3）求异面直线SC与AB所成角的大小
如图,四棱锥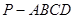
的底面是边长为
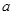的菱形,
,
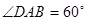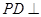平面
,
.
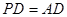（1）求直线PB与平面PDC所成的角的正切值;
（2）求二面角A－PB－D的大小.
（本小题满分12分）
已知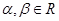
，写出用
表示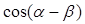
的关系等式，并证明这个关系等式．
（本小题满分10分）
如图，在直三棱柱
中，
，
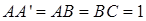．棱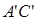
上有两个动点E，F，且EF =" a" （a为常数）．
（Ⅰ）在平面ABC内确定一条直线，使该直线与直线CE垂直；
（Ⅱ）判断三棱锥B—CEF的体积是否为定值．若是定值，求出这个三棱锥的体积；若不是定值，说明理由．