设全集是实数集R,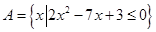 ,
,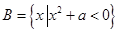 。
。
⑴当 ,求
,求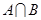 ,
,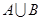 。
。
⑵若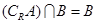 ,求实数
,求实数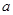 的取值范围.
的取值范围.
(本小题满分12分)已知函数 ,
,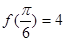 ,
,
(1)求实数a的值;(2)求函数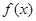 在
在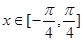 的值域。
的值域。
设数列 为等差数列,且
为等差数列,且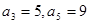 ;数列
;数列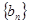 的前n项和为
的前n项和为 ,且
,且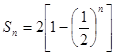 .
.
(Ⅰ)求数列 ,
,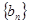 的通项公式;
的通项公式;
(Ⅱ)若 ,
,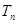 为数列
为数列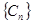 的前n项和,求
的前n项和,求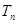
设{an}是公比为 q的等比数列,且a1,a3,a2成等差数列.
(Ⅰ)求q的值;
(Ⅱ)设{bn}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
在 中角A、B、C所对的边分别为a、b、c,面积为S.已知
中角A、B、C所对的边分别为a、b、c,面积为S.已知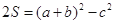
(Ⅰ)求 ;
;
(Ⅱ)若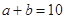 ,求S的最大值.
,求S的最大值.
一个盒子里装有三张卡片,分别标记有数字 ,
,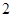 ,
, ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取 次,每次抽取
次,每次抽取 张,将抽取的卡片上的数字依次记为
张,将抽取的卡片上的数字依次记为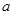 ,
, ,
,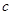 .
.
(Ⅰ)求“抽取的卡片上的数字满足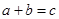 ”的概率;
”的概率;
(Ⅱ)求“抽取的卡片上的数字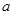 ,
, ,
,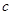 不完全相同”的概率.
不完全相同”的概率.