如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱 ,
, ,底面
,底面 为直角梯形,其中BC∥AD, AB⊥AD,
为直角梯形,其中BC∥AD, AB⊥AD,  ,O为AD中点.
,O为AD中点.
(1)求直线 与平面
与平面 所成角的余弦值;
所成角的余弦值;
(2)求 点到平面
点到平面 的距离
的距离
(3)线段 上是否存在点
上是否存在点 ,使得二面角
,使得二面角 的余弦值为
的余弦值为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知椭圆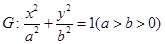 的离心率为
的离心率为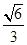 ,右焦点为(
,右焦点为(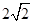 ,0),斜率为1的直线
,0),斜率为1的直线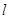 与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为P(-3,2).
与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为P(-3,2).
(Ⅰ)求椭圆G的方程;
(Ⅱ)求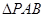 的面积.
的面积.
三棱柱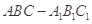 ,
,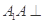 底面
底面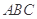 ,且
,且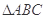 为正三角形,且,
为正三角形,且,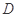 为
为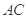 中点.
中点.
(1)求证:平面 ⊥平面
⊥平面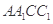
(2)若AA1=AB=2,求点A到面BC1D的距离.
某单位为了了解用电量y度与气温x0C之间的关系随机统计了某4天的用电量与当天气温
| 气温(0C) |
14 |
12 |
8 |
6 |
| 用电量 |
22 |
26 |
34 |
38 |
(1)求用电量y与气温x的线性回归方程;
(2)由(1)的方程预测气温为50C时,用电量的度数。
参考公式:
已知抛物线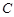 :
: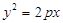 和⊙
和⊙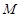 :
: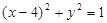 ,圆心
,圆心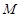 到抛物线准线的距离为6
到抛物线准线的距离为6
(1)求抛物线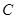 的方程;
的方程;
(2)求以抛物线C的焦点为右顶点,且离心率为2的双曲线C1的方程
如图,在正方体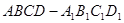 中,
中,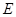 ,
,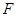 分别为棱
分别为棱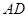 ,
,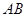 的中点.
的中点.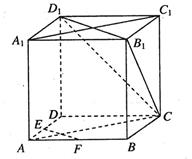
(1)求证: ∥平面
∥平面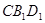 ;
;
(2)求CB1与平面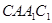 所成角的正弦值.
所成角的正弦值.