(本题12分)在人流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱.
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
等差数列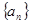 的前
的前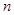 项和为
项和为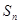 ,已知
,已知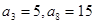 .
.
(1)求通项公式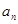 ;
;
(2)若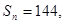 求
求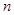 .
.
已知函数
,其中
是实数,设
,
为该函数图象上的点,且
.
(I)指出函数
的单调区间;
(II)若函数
的图象在点
处的切线互相垂直,且
,求
的最小值;
(III)若函数
的图象在点
处的切线重合,求
取值范围.
已知椭圆
(
)的两个焦点分别为
,
,且椭圆
经过点
.
(I)求椭圆
的离心率:
(II)设过点
的直线
与椭圆
交于
两点,点
是线段
上的点,且
,求点
的轨迹方程.
如图,在三棱柱
中,侧棱
底面
,
,
120°,
分别是线段
的中点,
是线段
的中点.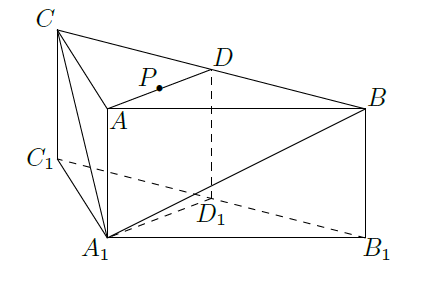
(I)在平面
内,试做出过点
与平面
平行的直线
,说明理由,并证明直线
平面
;
(II)设(I)中的直线
交
于点
,交
于点
,求二面角
的余弦值.
某算法的程序框图如图所示,其中输入的变量 在1,2,3,…,24这24个整数中等可能随机产生
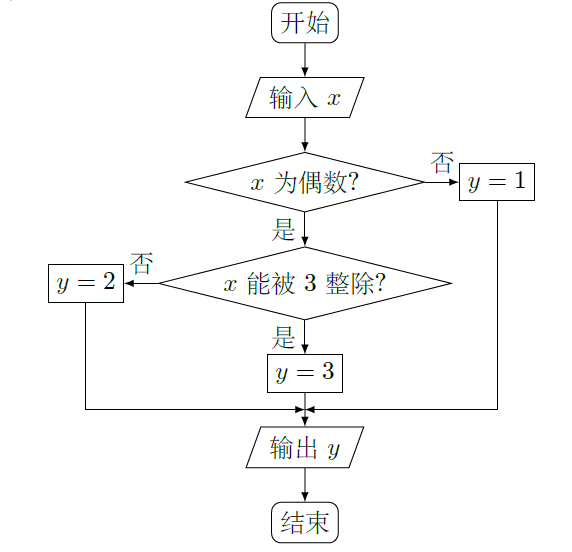
(I)分别求出按程序框图正确编程运行时输出
的值为
的概率
;
(II)甲乙两同学依据自己对程序框图的理解,各自编程写出程序重复运行
次后,统计记录输出y的值为
的频数,以下是甲乙所作频数统计表的部分数据.
甲的频数统计图(部分)
| 运行次数 | 输出
的值为1的频数 |
输出
的值为2的频数 |
输出
的值为3的频数 |
| 30 |
14 |
6 |
10 |
| … |
… |
… |
… |
| 2100 |
1027 |
376 |
697 |
乙的频数统计图(部分)
| 运行次数 | 输出
的值为1的频数 |
输出y的值为2的频数 |
输出
的值为3的频数 |
| 30 |
12 |
11 |
7 |
| … |
… |
… |
… |
| 2100 |
1051 |
696 |
353 |
当
时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为
的频率(用分数表示),并判断两位同学中哪一位所编程序符合要求的可能系较大;
(III)将按程序摆图正确编写的程序运行3次,求输出
的值为2的次数
的分布列及数学期望.