如图,在三棱柱
中,侧棱
底面
,
,
120°,
分别是线段
的中点,
是线段
的中点.
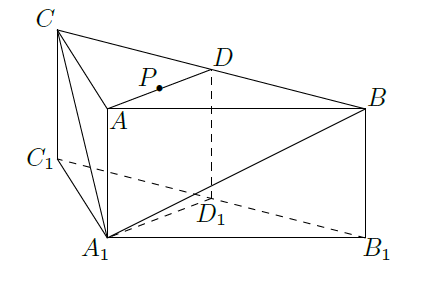
(I)在平面
内,试做出过点
与平面
平行的直线
,说明理由,并证明直线
平面
;
(II)设(I)中的直线
交
于点
,交
于点
,求二面角
的余弦值.
在△ABC中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,c.已知
,c.已知 .
.
(1)求角 的大小;
的大小;
(2)设 ,求T的取值范围.
,求T的取值范围.
如图,在四棱锥 中,底面
中,底面 是矩形,四条侧棱长均相等.
是矩形,四条侧棱长均相等.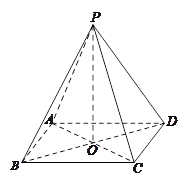
(1)求证:
 平面
平面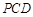 ;
;
(2)求证:平面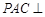 平面
平面 .
.
设函数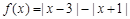 ,
,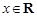 .
.
(1) 解不等式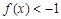 ;
;
(2) 设函数 ,且
,且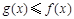 在
在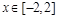 上恒成立,求实数
上恒成立,求实数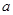 的取值范围.
的取值范围.
在极坐标系内,已知曲线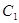 的方程为
的方程为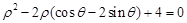 ,以极点为原点,极轴方向为
,以极点为原点,极轴方向为 正半轴方向,利用相同单位长度建立平面直角坐标系,曲线
正半轴方向,利用相同单位长度建立平面直角坐标系,曲线 的参数方程为
的参数方程为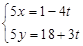 (
(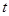 为参数).
为参数).
(1) 求曲线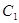 的直角坐标方程以及曲线
的直角坐标方程以及曲线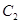 的普通方程;
的普通方程;
(2) 设点 为曲线
为曲线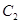 上的动点,过点
上的动点,过点 作曲线
作曲线 的两条切线,求这两条切线所成角余弦值的取值范围.
的两条切线,求这两条切线所成角余弦值的取值范围.
如图, 是
是 的切线,
的切线,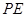 过圆心
过圆心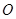 ,
, 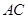 为
为 的直径,
的直径, 与
与 相交于
相交于 、
、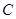 两点,连结
两点,连结 、
、 . (1) 求证:
. (1) 求证: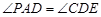 ;
;
(2) 求证: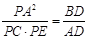 .
.