某校举办一场篮球投篮选拔比赛，比赛的规则如下：每个选手先后在二分区、三分区和中场跳球区三个位置各投一球，只有当前一次球投进后才能投下一次，三次全投进就算胜出，否则即被淘汰. 已知某选手在二分区投中球的概率为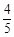
，在三分区投中球的概率为
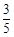，在中场跳球区投中球的概率为
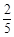，且在各位置投球是否投进互不影响.
（Ⅰ）求该选手被淘汰的概率；
（Ⅱ）该选手在比赛中投球的个数记为ξ，求随机变量ξ的分布列与数学期望Eξ.（注：本小题结果可用分数表示）
设
，求
．
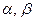（本小题满分16分）已知函数
（1）若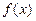
是区间（0，1）上单调函数，求
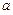的取值范围；
（2）若
，试求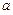的取值范围。
（本小题满分14分）如图，三棱柱ABC—A1B1C1中，AA1
面ABC，BCAC，BC=AC=2，D为AC的中点。[
（1）求证：AB1//面BDC1；
（2）若AA1=3，求二面角C1—BD—C的余弦值；
（3）若在线段AB1上存在点P，使得CP面BDC1，试求AA1的长及点P的位置。
（本小题满分14分）已知
抛物线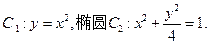
（1）设
是C1的任意两条互相垂直的切线，并设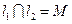
，证明
：点M的纵坐标为定值；
（2）在C1上是否存在点P，使得C1在点P处切线与C2相交于两点A、B，且AB的中垂线恰为C1的切线？若存在，求出点P的坐标；若不存在，说明理由。
（本小题满分14分）质地均匀的正四面体玩具的4个面上分别刻着数字1，2，3，4，将4个这样的玩具同时抛掷于桌面上。
（1）求与桌面接触的4个面上的4个数的乘积不能被4整除的概率；
（2）设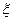
为与桌面接触的4个面上数字中偶数的个数，求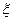的分歧布列及期望E。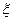