(本小题满分12分)已知A,B两点是椭圆 与坐标轴正半轴的两个交点.
与坐标轴正半轴的两个交点.
(1)设 为参数,求椭圆的参数方程;
为参数,求椭圆的参数方程;
(2)在第一象限的椭圆弧上求一点P,使四边形OAPB的面积最大,并求此最大值.
已知等比数列 中,
中, .若
.若 ,数列
,数列 前
前 项的和为
项的和为 .
.
(Ⅰ)若 ,求
,求 的值;
的值;
(Ⅱ)求不等式 的解集.
的解集.
在 中,内角
中,内角 对边的边长分别是
对边的边长分别是 ,已知
,已知 ,
,
(Ⅰ)若 ,求
,求 ;
;
(Ⅱ)若 的面积等于
的面积等于 ,求
,求 。
。
已知 为等差数列,且
为等差数列,且 ,
, 。
。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若等比数列 满足
满足 ,
, ,求数列
,求数列 的前n项和
的前n项和 。
。
已知不等式 的解集为
的解集为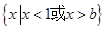

(Ⅰ)求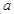 、
、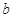 的值;
的值;
(Ⅱ)解不等式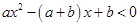 .
.
学校食堂定期向精英米业以每吨1500元的价格购买大米,每次购买大米需支付运输费用100元,已知食堂每天需食用大米1吨,储存大米的费用为每吨每天2元,假设食堂每次均在用完大米的当天购买.
(1)问食堂每隔多少天购买一次大米,能使平均每天所支付的费用最少?
(2)若购买量大,精英米业推出价格优惠措施,一次购买量不少于20吨时可享受九五折优惠,问食堂能否接受此优惠措施?请说明理由.