对于代数式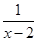 和
和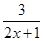 ,你能找到一个合适的
,你能找到一个合适的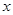 值,使它们的值相等吗?写出你的解题过程.
值,使它们的值相等吗?写出你的解题过程.
(1)化简: ;
(2)解不等式组 ,并写出它的正整数解.
请用直尺、圆规作图,不写作法,但要保留作图痕迹.
已知: ,直线 及 上两点 , .
求作: ,使点 在直线 的上方,且 , .

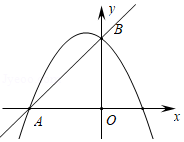
在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 ,抛物线 经过点 、 .
(1)求 、 满足的关系式及 的值.
(2)当 时,若 的函数值随 的增大而增大,求 的取值范围.
(3)如图,当 时,在抛物线上是否存在点 ,使 的面积为1?若存在,请求出符合条件的所有点 的坐标;若不存在,请说明理由.
如图,在正方形 中, 是 边上一点,(与 、 不重合),连接 ,将 沿 所在的直线折叠得到 ,延长 交 于 ,连接 ,作 ,与 的延长线交于点 ,连接 .显然 是 的平分线, 是 的平分线.仔细观察,请逐一找出图中其他的角平分线(仅限于小于 的角平分线),并说明理由.

汛期到来,山洪暴发.下表记录了某水库 内水位的变化情况,其中 表示时间(单位: , 表示水位高度(单位: ,当 时,达到警戒水位,开始开闸放水.
|
|
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
|
14 |
15 |
16 |
17 |
18 |
14.4 |
12 |
10.3 |
9 |
8 |
7.2 |
(1)在给出的平面直角坐标系中,根据表格中的数据描出相应的点.
(2)请分别求出开闸放水前和放水后最符合表中数据的函数解析式.
(3)据估计,开闸放水后,水位的这种变化规律还会持续一段时间,预测何时水位达到 .
