小虫从某点0出发在一直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,爬过的各段路程依次为(单位:厘米):+5,-3,+10,-8,-6,+12,-10,求
(1) 小虫最后是否回到出发点“0” ?为什么?
(2) 小虫离开出发点“0”最远时是多少厘米?
(3) 在爬行过程中,如果爬1厘米奖励两粒芝麻,那么小虫一共能得到多少粒芝麻?
如图,点 是反比例函数 图象上一点,过点 分别向坐标轴作垂线,垂足为 , .反比例函数 的图象经过 的中点 ,与 , 分别相交于点 , .连接 并延长交 轴于点 ,点 与点 关于点 对称,连接 , .
(1)填空: ;
(2)求 的面积;
(3)求证:四边形 为平行四边形.

某社区拟建 , 两类摊位以搞活"地摊经济",每个 类摊位的占地面积比每个 类摊位的占地面积多2平方米.建 类摊位每平方米的费用为40元,建 类摊位每平方米的费用为30元.用60平方米建 类摊位的个数恰好是用同样面积建 类摊位个数的 .
(1)求每个 , 类摊位占地面积各为多少平方米?
(2)该社区拟建 , 两类摊位共90个,且 类摊位的数量不少于 类摊位数量的3倍.求建造这90个摊位的最大费用.
如图1,在四边形 中, , , 是 的直径, 平分 .
(1)求证:直线 与 相切;
(2)如图2,记(1)中的切点为 , 为优弧 上一点, , .求 的值.

已知关于 , 的方程组 与 的解相同.
(1)求 , 的值;
(2)若一个三角形的一条边的长为 ,另外两条边的长是关于 的方程 的解.试判断该三角形的形状,并说明理由.
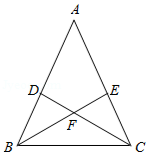
如图,在 中,点 , 分别是 、 边上的点, , , 与 相交于点 .求证: 是等腰三角形.