如图,曲线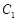 是以原点O为中心、
是以原点O为中心、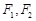 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线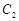 是以O为顶点、
是以O为顶点、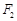 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线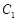 和
和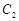 的交点
的交点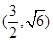 且
且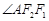 为钝角.
为钝角. 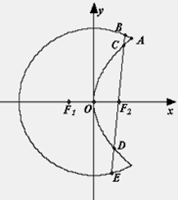
(1)求曲线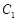 和
和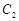 的方程;
的方程;
(2)过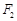 作一条与
作一条与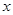 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线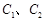 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问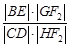 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由.
(本小题满分12分)
如图,直角梯形ABCD中,∠B=90°,AD//BC,AD=1,BC=2,
∠C=60°,将该梯形绕着AB所在的直线为轴旋转一周,求该旋转体的表面积和体积。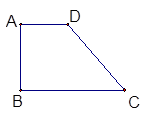
(本小题满分11分)
已知直线m过点(-1,2),且垂直于 : x+2y+2=0
: x+2y+2=0
(1)求直线m;
(2)求直线m和直线l的交点。
已知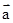 =(sinθ,1),
=(sinθ,1), =(1,cosθ),
=(1,cosθ),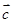 =(0,3),
=(0,3), <θ<
<θ< .
.
(1)若(4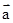 -
-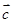 )∥
)∥ ,求θ;
,求θ;
(2)求|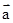 +
+ |的取值范围.
|的取值范围.
设两非零向量e1和e2不共线.
(1)如果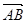 =
=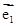 +
+ ,
,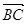 =2
=2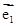 +8
+8 ,
, =3(
=3(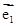 -
- ),求证:A、B、D三点共线;
),求证:A、B、D三点共线;
(2)试确定实数k,使k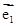 +
+ 和
和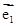 +k
+k 共线;
共线;
(3)若|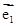 |=2,|
|=2,| |=3,
|=3,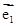 与
与 的夹角为60°,试确定k的值,使k
的夹角为60°,试确定k的值,使k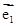 +
+ 与
与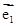 +k
+k 垂直.
垂直.
已知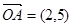 ,
, ,
, ,在
,在 上是否存在点M,使
上是否存在点M,使 ,若存在,求出点M的坐标;若不存在,请说明理由.
,若存在,求出点M的坐标;若不存在,请说明理由.