(本小题满分11分)
已知直线m过点(-1,2),且垂直于 : x+2y+2=0
: x+2y+2=0
(1)求直线m;
(2)求直线m和直线l的交点。
本题文科生做.
已知复数 ,若
,若 ,求
,求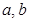 的值.
的值.
已知函数 ,
, ,其中
,其中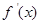 是
是 的导函数.
的导函数.
(1)对满足 的一切
的一切 的值,都有
的值,都有 ,求实数
,求实数 的取值范围;
的取值范围;
(2)设 ,当实数
,当实数 在什么范围内变化时,函数
在什么范围内变化时,函数 的图象与直线
的图象与直线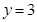 只有一个公共点.
只有一个公共点.
(本小题满分16分)
某市近郊有一块大约500m×500m的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米。
(1)分别用x表示y和S的函数关系式,并给出定义域;
(2)怎样设计能使S取得最大值,并求出最大值。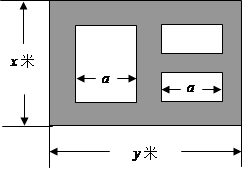
本题理科做.
设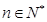 ,
,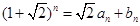 (
(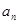 、
、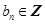 )。
)。
(1)求出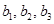 的值;
的值;
(2)求证:数列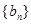 的各项均为奇数.
的各项均为奇数.
本题文科做.
已知二次函数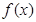 的二次项系数为
的二次项系数为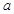 ,且不等式
,且不等式 的解集为
的解集为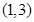 .
.
(1)若方程 有两个相等的实数根, 求
有两个相等的实数根, 求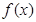 的解析式;
的解析式;
(2)若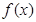 的最大值为正数,求
的最大值为正数,求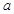 的取值范围.
的取值范围.