为了美化校园环境，建设绿色校园，某学校准备对校园中30亩空地进行绿化..绿化采用种植草皮与种植树木两种方式，要求种植草皮与种植树木的面积都不少于10亩，并且种植草皮面积不少于种植树木面积的
.已知种植草皮与种植树木每亩的费用分别为8000元与12000元.
（1）种植草皮的最小面积是多少？
（2）种植草皮的面积为多少时绿化总费用最低？最低费用为多少？
如图，
在方格纸中
（1）请在方格纸上建立平面直角坐标系，使
，并求出
点坐标；
（2）以原点
为位似中心，相似比为2，在第一象限内将放大，画出放大后的图形
；
（3）计算的面积
．
若关于x的分式方程
－
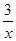=1无解，求m的值。
先化简
，再从-2 ， 2，
中选择一个合适的数代入求值.
⑴解不等式组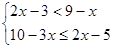
⑵解方程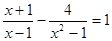
阅读理解：对于任意正实数a、b，∵(
－
)2≥0，∴a－2
＋b≥0，∴a＋b≥2，只有当a＝b时，等号成立.
结论：在a＋b≥2（a、b均为正实数）中，若ab为定值p，则a+b≥2
，只有当a＝b时，a＋b有最小值2.根据上述内容，回答下列问题：
（1）若m＞0，只有当m＝时，m＋
有最小值；
若m＞0，只有当m＝时，2m＋
有最小值.
（2）如图，已知直线L1：y＝
x＋1与x轴交于点A，过点A的另一直线L2与双曲线y＝
（x>0）相交于点B（2，m），求直线L2的解析式.
（3）在（2）的条件下，若点C为双曲线上任意一点，作CD∥y轴交直线L1于点D，试
求当线段CD最短时，点A、B、C、D围成的四边形面积.