有10箱苹果,标准质量是每箱25千克,每箱质量与标准质量的差值(单位:千克)
如下:0.25,0,-0.4,0,0,0.2,0.3,-0.3,0,0. 苹果总共有多少千克?
如图,已知c<0,抛物线y=x2+bx+c与x轴交于A(x1,0),B(x2,0)两点(x2>x1),与y轴交于点C.
(1)若x2=1,BC= ,求函数y=x2+bx+c的最小值;
,求函数y=x2+bx+c的最小值;
(2)过点A作AP⊥BC,垂足为P(点P在线段BC上),AP交y轴于点M.若 =2,求抛物线y=x2+bx+c顶点的纵坐标随横坐标变化的函数解析式,并直接写出自变量的取值范围.
=2,求抛物线y=x2+bx+c顶点的纵坐标随横坐标变化的函数解析式,并直接写出自变量的取值范围.
已知A,B,C,D是⊙O上的四个点.
(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;
(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.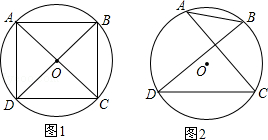
当m,n是正实数,且满足m+n=mn时,就称点P(m, )为“完美点”,已知点A(0,5)与点M都在直线y=﹣x+b上,点B,C是“完美点”,且点B在线段AM上,若MC=
)为“完美点”,已知点A(0,5)与点M都在直线y=﹣x+b上,点B,C是“完美点”,且点B在线段AM上,若MC=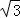 ,AM=4
,AM=4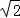 ,求△MBC的面积.
,求△MBC的面积.
已知锐角三角形ABC,点D在BC的延长线上,连接AD,若∠DAB=90°,∠ACB=2∠D,AD=2,AC= ,根据题意画出示意图,并求tanD的值.
,根据题意画出示意图,并求tanD的值.
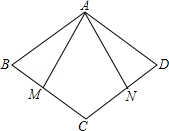
如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD,AM=AN,求证:四边形ABCD是菱形.