如果实数x、y满足x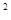 +y
+y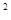 -4x+1=0,求
-4x+1=0,求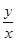 的最大值与最小值。
的最大值与最小值。
(本小题满分12分)
某中学共有1000名学生参加了该地区高三第一次质量检测的数学考试,数学成绩如下表所示:
| 数学成绩分组 |
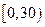 |
 |
 |
 |
 |
| 人数 |
60 |
90 |
300 |
x |
160 |
(I)为了了解同学们前段复习的得失,以便制定下阶段的复习计划,学校将采用分层抽
样的方法抽取100名同学进行问卷调查,甲同学在本次测试中数学成绩为95分,
求他被抽中的概率;
(II)已知本次数学成绩的优秀线为110分,试根据所提供数据估计该中学达到优秀线的人数;
(III)作出频率分布直方图,并估计该学校本次考试的数学平均分。
(本小题满分12分)
某中学共有1000名学生参加了该地区高三第一次质量检测的数学考试,数学成绩如下表所示:
| 数学成绩分组 |
 |
 |
 |
 |
 |
| 人数 |
60 |
90 |
300 |
x |
160 |
(I)为了了解同学们前段复习的得失,以便制定下阶段的复习计划,学校将采用分层抽
样的方法抽取100名同学进行问卷调查,甲同学在本次测试中数学成绩为95分,
求他被抽中的概率;
(II)已知本次数学成绩的优秀线为110分,试根据所提供数据估计该中学达到优秀线的人数;
(III)作出频率分布直方图,并估计该学校本次考试的数学平均分。(同一组中的数据用该组区间的中点值作代表)
(本小题满分1 0分)选修4-1:几何证明选讲
0分)选修4-1:几何证明选讲
如图,AB是⊙O的直径,C、F为⊙O上的点,CA是∠BAF的角平分线,过点C
作CD⊥AF交AF的延长线于D点,CM⊥AB,垂足为点M。
(I)求证:DC是⊙O的切线;
(II)求证:AM:MB=DF·DA。
(本小题满分12分)
已知圆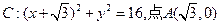 ,Q是圆上一动点,AQ的垂直平分线交CQ于点M,设点M的轨迹为E。
,Q是圆上一动点,AQ的垂直平分线交CQ于点M,设点M的轨迹为E。
(I)求轨迹E的方程;
(II)过点P(1,0)的直线 交轨迹E于两个不同的点A、B,
交轨迹E于两个不同的点A、B, (O是坐标原点)的面积
(O是坐标原点)的面积 ,求直线AB的方程。
,求直线AB的方程。
(本小题满分12分)
已知函数
(I)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(II)求证: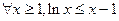 ;
;
(III)已知数列 若
若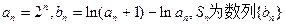 的前n项和,求证:
的前n项和,求证: