已知函数 ,其中
,其中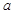 为正实数,
为正实数,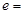 2.7182……
2.7182……
(1)当 时,求
时,求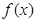 在点
在点 处的切线方程。
处的切线方程。
(2)是否存在非零实数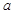 ,使
,使 恒成立。
恒成立。
设命题 :函数
:函数 在
在 上为减函数,命题
上为减函数,命题 :
: 的值域为R,命题
的值域为R,命题 :函数
:函数 的定义域为R,
的定义域为R,
(1)若命题 为真命题,求
为真命题,求 的取值范围;
的取值范围;
(2)若 或
或 为真命题,
为真命题, 且
且 为假命题,求
为假命题,求 的取值范围.
的取值范围.
如图所示,已知空间四边形 的每条边和对角线长都等于1,点
的每条边和对角线长都等于1,点 ,
, ,
, 分别是
分别是 、
、 、
、 的中点,计算:
的中点,计算:
(1) ;
;
(2) 的长;
的长;
(3)异面直线 与
与 所成角的余弦值.
所成角的余弦值.
一变压器的铁芯截面为正十字型,为保证所需的磁通量,要求十字应具有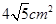 的面积,问应如何设计十字型宽
的面积,问应如何设计十字型宽 及长
及长 ,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜钱最节省.
,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜钱最节省.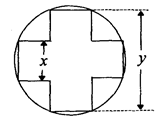
设命题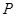 :“
:“ ”,命题
”,命题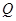 :“
:“ ”;如果“
”;如果“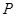 或
或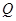 ”为真,“
”为真,“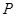 且
且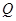 ”为假,求
”为假,求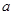 的取值范围.
的取值范围.
设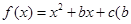 、
、 .
.
(Ⅰ)若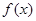 在
在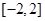 上单调,求
上单调,求 的取值范围;
的取值范围;
(Ⅱ)若 对一切
对一切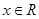 恒成立,求证:
恒成立,求证: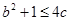 ;
;
(Ⅲ)若对一切满足 的实数
的实数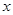 ,都有
,都有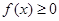 ,且
,且 的最大值为1,求证:
的最大值为1,求证: 、
、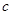 满足的条件是
满足的条件是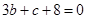 且
且