为了保护水资源,提倡节约用水,某市对居民生活用水收费标准如下:每户每月用水不超过6吨时每吨3元,当用水超过6吨但不超过15吨时,超过部分每吨5元,当用水超过15吨时,超过部分每吨10元。
(1)求水费y(元)关于用水量x(吨)之间的函数关系式;
(2)若某户居民某月所交水费为93元,试求此用户该月的用水量。
已知函数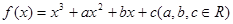 的图像过原点,且在
的图像过原点,且在 处的切线为直线
处的切线为直线
(Ⅰ)求函数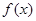 的解析式;
的解析式;
(Ⅱ)求函数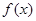 在区间
在区间 上的最小值和最大值.
上的最小值和最大值.
已知 .
.
(1)若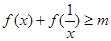 恒成立,求
恒成立,求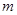 的最大值;
的最大值;
(2)若 为常数,且
为常数,且 ,记
,记 ,求
,求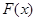 的最小值.
的最小值.
(如图1)在平面四边形 中,
中,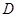 为
为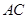 中点,
中点, ,
, ,且
,且 ,现沿
,现沿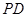 折起使
折起使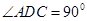 ,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.
,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.
(1)求三棱锥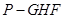 的体积;
的体积;
(2)在线段PC上是否存在一点M,使直线 与直线
与直线 所成角为
所成角为 ?若存在,求出线段的长;若不存在,请说明理由.
?若存在,求出线段的长;若不存在,请说明理由.
已知函数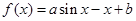 (
( 均为正常数),设函数
均为正常数),设函数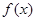 在
在 处有极值.
处有极值.
(1)若对任意的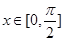 ,不等式
,不等式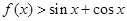 总成立,求实数
总成立,求实数 的取值范围;
的取值范围;
(2)若函数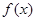 在区间
在区间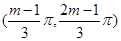 上单调递增,求实数
上单调递增,求实数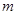 的取值范围.
的取值范围.
已知数列 为等差数列,数列
为等差数列,数列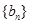 为等比数列,若
为等比数列,若 ,且
,且 .
.
(1)求数列 ,
,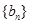 的通项公式;
的通项公式;
(2)是否存在 ,使得
,使得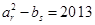 ,若存在,求出所有满足条件的
,若存在,求出所有满足条件的 ;若不存在,请说明理由.
;若不存在,请说明理由.