化简下列分数：
（1）
；（2）
；（3）
；（4）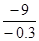
.
如图1，已知抛物线y=－x2+bx+c经过点A（1,0），B（－3,0）两点，且与y轴交于点C.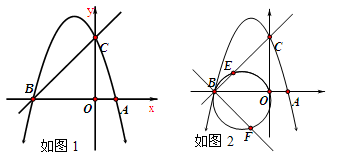
（1）求b，c的值。
（2）在第二象限的抛物线上，是否存在一点P，使得△PBC的面积最大？求出点P的坐标及△PBC的面积最大值.若不存在，请说明理由.
（3）如图2，点E为线段BC上一个动点（不与B,C重合），经过B、E、O三点的圆与过点B且垂直于BC的直线交于点F，当△OEF面积取得最小值时，求点E坐标．
如图，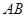
为⊙O的直径，
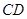为弦，且
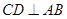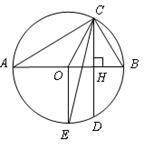
，垂足为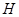
．
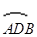（1）如果⊙O的半径为4，
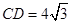，求
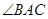的度数；
（2）若点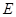
为的中点，连结
，
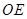．求证：平分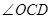
；
（3）在（1）的条件下，圆周上到直线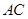
距离为3的点有多少个？并说明理由．
正方形网格中，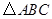
为格点三角形（顶点都是格点），将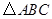绕点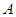
按逆时针方向旋转
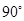得到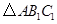
．
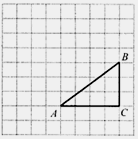
（1）在正方形网格中，作出；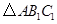
（2）设网格小正方形的边长为1，求旋转过程中动点B经过的路线长和
AC
所扫过的面积．
某商场以每件20元的价格购进一种商品，试销中发现，这种商品每天的销售量m（件）与每件的销售价x（元）满足关系：m=140－2x.
（1）写出商场卖这种商品每天的销售利润y（元）与x（元）间的函数关系式，并写出x的取值范围；
（2）若商场要使每天获得的利润最大，每件商品的售价定为多少？
如图所示，已知AB为⊙O的直径，CD是弦，且AB
CD于点E．连接AC、OC、BC．
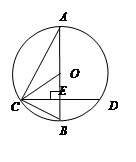
（1）求证：
ACO=BCD．
（2）若EB=8cm，CD=24cm，求⊙O的直径．