顾客李某于今年“五·一”期间到电器商场购买空调,与营业员有如下的一段对话:
顾客李某:A品牌的空调去年“国庆”期间价格为3000元,这次便宜多了,一次就降为2430元,是不是质量有问题?
营业员:不是一次降价,这是第二次降价,今年春节期间已经降了一次价,两次降价的幅度相同.我们所销售的空调质量都是很好的,尤其是A品牌系列空调的质量是一流的.
顾客李某:我们单位的同事也想买一台A品牌的空调,有优惠政策吗?
营业员:有,请看《购买A品牌系列空调的优惠办法》.购买A品牌系列空调的优惠办法:
方案一:各种型号的空调每台价格优惠5%,送货上门,负责安装,每台空调另加运输费和安装费共90元.
方案二:各种型号的空调每台价格优惠2%,送货上门,负责安装,免运输费和安装费.根据以上对话和A品牌系列空调销售的优惠办法,请你回答下列问题:
(1)求A品牌系列空调平均每次降价的百分率?
(2)请你为顾客李某决策,选择哪种优惠更合算,并通过计算说明。
解方程: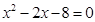
点P在图形M上, 点Q在图形N上,记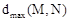 为线段PQ长度的最大值,
为线段PQ长度的最大值,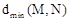 为线段PQ长度的最小值,图形M,N的平均距离
为线段PQ长度的最小值,图形M,N的平均距离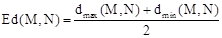 .
.
(1)在平面直角坐标系 中,⊙O是以O为圆心,2的半径的圆,且A
中,⊙O是以O为圆心,2的半径的圆,且A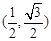 ,B
,B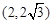 ,求
,求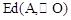 及
及 ;(直接写出答案即可)
;(直接写出答案即可)
(2)半径为1的⊙C的圆心C与坐标原点O重合,直线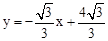 与
与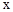 轴交于点D,与
轴交于点D,与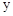 轴交于点F,记线段DF为图形G,求
轴交于点F,记线段DF为图形G,求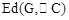 ;
;
(3)在(2)的条件下,如果⊙C的圆心C从原点沿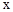 轴向右移动,⊙C的半径不变,且
轴向右移动,⊙C的半径不变,且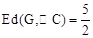 ,求圆心C的横坐标.
,求圆心C的横坐标.
在△ABC中,AB=AC,∠BAC<60°,把线段BC绕点B逆时针旋转60°至BP;如图所示位置有∠ABQ=60°,∠BCQ=150°.
(1)若∠BAC=30°,则∠ABP=度;若∠BAC=α,则∠ABP=(用α表示);
(2)求证:△ABQ为等边三角形;
(3)四边形CBPQ的面积为1,求△ABC的面积.
已知关于 的一元二次方程
的一元二次方程 .
.
(1)若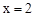 是该方程的一个根,求
是该方程的一个根,求 的值;
的值;
(2)无论 取任何值,该方程的根不可能为
取任何值,该方程的根不可能为 ,写出
,写出 的值,并证明;
的值,并证明;
(3)若 为正整数,且该方程存在正整数解,求所有正整数
为正整数,且该方程存在正整数解,求所有正整数 的值.
的值.
如图,已知点C、D在以O为圆心,AB为直径的半圆上,且OC⊥BD于点M,CF⊥AB于点F交BD于点E,BD=8,CM=2.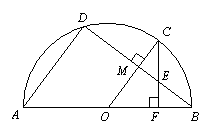
(1)求⊙O的半径;
(2)求证:CE=BE.