已知全体实数集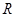 ,集合
,集合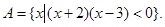
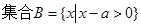
(1)若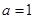 时,求
时,求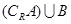 ;(2)设
;(2)设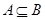 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分14分)
已知函数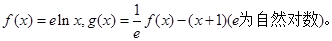
(1)求函数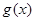 的极大值;
的极大值;
(2)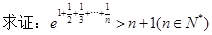
(3)对于函数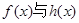 定义域上的任意实数
定义域上的任意实数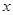 ,若存在常数
,若存在常数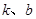 ,使得
,使得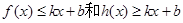 都成立,则称直线
都成立,则称直线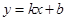 为函数
为函数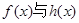 的分界线。设
的分界线。设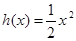 ,试探究函数
,试探究函数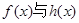 是否存在“分界线”?若存在,请给予证明,并求出
是否存在“分界线”?若存在,请给予证明,并求出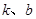 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(本小题满分14分)
设函数f(x)=tx2+2t2x+t-1(t∈R,t>0).
(1)求f(x)的最小值s(t);
(2)若s(t)<-2t+m对t∈(0,2)时恒成立,求实数m的取值范围.
(本小题满分14分)
已知数列{an}中,a1 =1,前 n项和为Sn,且点(an,an+1)在直线x-y+1=0上.
计算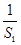 +
+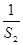 +
+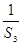 +…
+…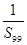
(本小题满分14分)
在△ABC中,BC=2,AB+AC=3,中线AD的长为y,AB的长为x,
(1)建立y与x的函数关系式,并指出其定义域.
(2)求y的最小值,并指出x的值.