已知直线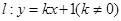 与椭圆
与椭圆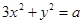 相交于
相交于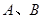 两个不同的点,记
两个不同的点,记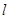 与
与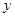 轴的交点为
轴的交点为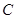 .
.
(Ⅰ)若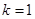 ,且
,且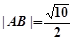 ,求实数
,求实数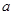 的值;
的值;
(Ⅱ)若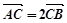 ,求
,求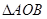 面积的最大值,及此时椭圆的方程.
面积的最大值,及此时椭圆的方程.
在四棱锥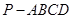 中,
中,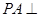 平面
平面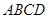 ,
,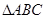 是正三角形,
是正三角形,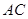 与
与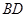 的交点
的交点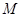 恰好是
恰好是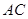 中点,又
中点,又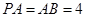 ,
,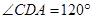 ,点
,点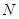 在线段
在线段 上,且
上,且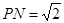 .
.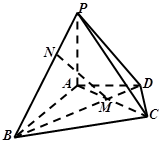
(Ⅰ)求证: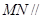 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面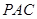 所成角的正弦值.
所成角的正弦值.
已知函数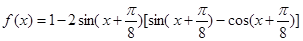 .
.
(Ⅰ)求函数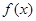 的最小正周期;
的最小正周期;
(Ⅱ)当 ,求函数
,求函数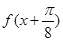 的值域.
的值域.
在数列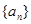 中,
中,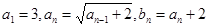 ,
,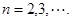
(Ⅰ)求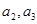 ,判断数列
,判断数列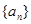 的单调性并证明;
的单调性并证明;
(Ⅱ)求证: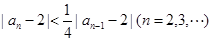 ;
;
(Ⅲ)是否存在常数 ,对任意
,对任意 ,有
,有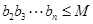 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
设二次函数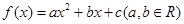 满足条件:①当
满足条件:①当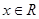 时,
时,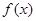 的最大值为0,且
的最大值为0,且 成立;②二次函数
成立;②二次函数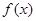 的图象与直线
的图象与直线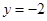 交于
交于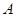 、
、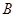 两点,且
两点,且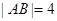 .
.
(Ⅰ)求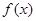 的解析式;
的解析式;
(Ⅱ)求最小的实数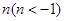 ,使得存在实数
,使得存在实数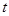 ,只要当
,只要当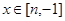 时,就有
时,就有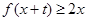 成立.
成立.