设全集为
，在下列条件中，哪些是
的充要条件？
（1）
；
（2）
；
（3）
．
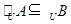已知数列{an}，其前n项和为Sn.
(1)若对任意的n∈N，a2n－1，a2n＋1，a2n组成公差为4的等差数列，且a1＝1，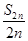
＝2013，求n的值；
(2)若数列
是公比为q(q≠－1)的等比数列，a为常数，求证：数列{an}为等比数列的充要条件为q＝1＋
.
设不等式组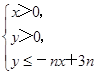
所表示的平面区域为Dn，记Dn内的整点个数为an(n∈N*)(整点即横坐标和纵坐标均为整数的点)．
(1)求数列{an}的通项公式；
(2)记数列{an}的前n项和为Sn，且Tn＝
.若对于一切的正整数n，总有Tn≤m，求实数m的取值范围．
已知数列{an}满足a1＋a2＋…＋an＝n2(n∈N*)．
(1)求数列{an}的通项公式；
(2)对任意给定的k∈N*，是否存在p，r∈N*(k<p<r)使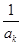
，
，
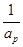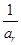成等差数列？若存在，用k分别表示p和r(只要写出一组)；若不存在，请说明理由．
正项数列{an}的前项和满足：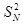
－(n2＋n－1)Sn－(n2＋n)＝0.
(1)求数列{an}的通项公式an；
(2)令bn＝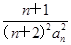
，数列{bn}的前n项和为Tn.证明：对于任意的n∈N*，都有Tn<
.
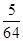设{an}是首项为a，公差为d的等差数列(d≠0)，Sn是其前n项和．记bn＝
，n∈N*，其中c为实数．
(1)若c＝0，且b1，b2，b4成等比数列，证明：Snk＝n2Sk(k，n∈N*)；
(2)若{bn}是等差数列，证明：c＝0.