设二次方程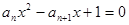 ,
,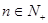 有两根
有两根 和
和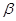 ,且满足
,且满足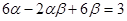 ,
, 
(1)试用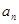 表示
表示 ; (2)证明
; (2)证明 是等比数列;
是等比数列;
(3)设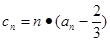 ,
,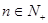 ,
, 为
为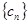 的前n项和,证明
的前n项和,证明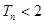 ,(
,(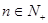 )。
)。
(本小题满分12分)
如图, 在直三棱柱ABC-A1B1C1中,AC=3 ,BC=4,
,BC=4, ,AA1=4,点D是AB的中点.
,AA1=4,点D是AB的中点.
(Ⅰ)求证:AC⊥BC1;
(Ⅱ)求二面角 的余弦值.
的余弦值.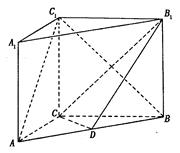
(本小题满分14分)
设函数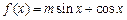
 的图象经过点
的图象经过点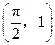 .
.
(Ⅰ)求 的解析式,并求函数的最小正周期和最值.
的解析式,并求函数的最小正周期和最值.
(Ⅱ)若 ,其中
,其中 是面积为
是面积为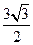 的锐角
的锐角 的内角,且
的内角,且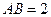 ,
,
求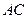 和
和 的长.
的长.
已知函数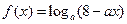
(1)若 ,求实数
,求实数 的取值范围;
的取值范围;
(2)若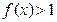 在区间[1,2]上恒成立,求实数
在区间[1,2]上恒成立,求实数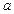 的取值范围.
的取值范围.
若数列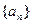 的前
的前 项和为
项和为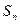 ,点
,点 均在函数
均在函数 的图象上
的图象上
(1)求数列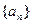 的通项公式;
的通项公式;
(2)若数列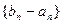 是首项为1,公比为
是首项为1,公比为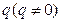 的等比数列,求数列
的等比数列,求数列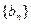 的前
的前 项和
项和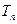 .
.
、如图,已知四棱锥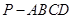 中,底面
中,底面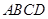 是直角梯形,
是直角梯形, ,
,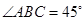 ,
,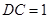 ,
,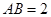 ,
, 平面
平面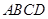 ,
,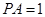 .
.
(1)求证: 平面
平面 ;
;
(2)求证: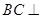 平面
平面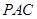 ;
;
(3)若M是PC的中点,求三棱锥M—ACD的体积.