（本小题满分13分）设椭圆
的左、右焦点分别为F1、F2，上顶点为A，在x轴上有一点B，满足
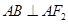且F1为BF2的中点.
（Ⅰ）求椭圆 C的离心率；
（Ⅱ）若过A、B、F2三点的圆恰好与直线
相切，判断椭圆C和直线
的位置关系.
如图,AB为⊙O的直径,直线CD与⊙O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连结AE,BE.证明:
(1)∠FEB=∠CEB;
(2)EF2=AD·BC.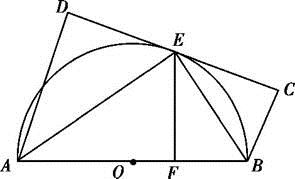
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.
(1)证明:DB=DC;
(2)设圆的半径为1,BC=
,延长CE交AB于点F,求△BCF外接圆的半径.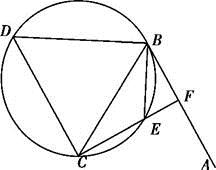
已知函数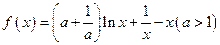
．
（1）讨论f(x)在区间（0，1）上的单调性；
（2）当a∈[3，+∞)时，曲线
上总存在相异的两点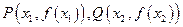
，使得曲线在点P，Q处的切线互相平行，求证：
．
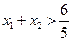已知函数
．
(1)若直线
与
的反函数的图象相切，求实数k的值;
(2)设
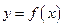，讨论曲线
与曲线
公共点的个数;
(3)设
，比较
与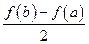
的大小，并说明理由．
已知动点P,Q都在曲线C: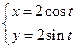 
(t为参数)上,对应参数分别为t=
与t=2(0<<2π),M为PQ的中点.
(1)求M的轨迹的参数方程;
(2)将M到坐标原点的距离d表示为的函数,并判断M的轨迹是否过坐标原点.