已知:x1,x2,…x2012都是不等于0的有理数,请你探究以下问题:
(1)若y1= ,则
,则 = ;
= ;
(2)若y2= ,则
,则 = ;
= ;
(3)若y3= ,则
,则 = ;
= ;
(4)由以上探究可知,y2012= ,
, 共有 个不同的值。请求出这些不同的y2012的值的绝对值的和。
共有 个不同的值。请求出这些不同的y2012的值的绝对值的和。
奶奶提一篮子玉米到集贸市场去兑换大米,每2kg玉米兑换1kg大米,商贩用秤称得连篮子带玉米恰好20kg,于是商贩连篮子带大米给奶奶共10kg,在这个过程中谁吃亏?吃亏有多大?(设合适的字母,然后用字母表示)
下图是一个数字转换机,请解答下列问题: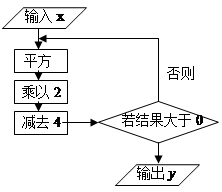
(1)填空:若输入的x值为2,则输出的y值为
(2)若输入的x值为1,则输出的y值为
(3)若输出的y值为28,那么输入的x值是什么?(写出三个x值,并写出简要的分析过程.)
如图,大正方形的边长为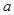 ,小正方形的边长为b,
,小正方形的边长为b,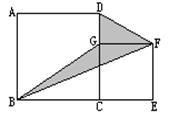
(1)用代数式表示阴影部分的面积;
(2)当a=10,b=4时,求阴影部分的面积.
先化简再求值: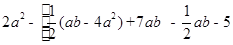 ,其中
,其中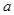 =2b
=2b