如图,已知椭圆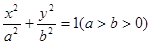 的长轴为
的长轴为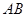 ,过点
,过点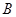 的直线
的直线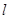 与
与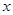 轴垂直,直线
轴垂直,直线 所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率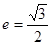
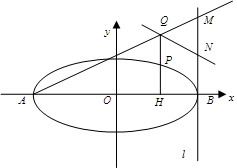
(1)求椭圆的标准方程;
(2)设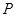 是椭圆上异于
是椭圆上异于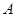 、
、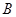 的任意一点,
的任意一点,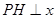 轴,
轴, 为垂足,延长
为垂足,延长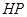 到点
到点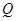 使得
使得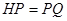 ,连接
,连接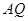 并延长交直线
并延长交直线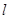 于点
于点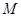 ,
,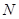 为
为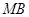 的中点.试判断直线
的中点.试判断直线 与以
与以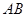 为直径的圆
为直径的圆 的位置关系.
的位置关系.
如图所示,在△ABO中, =
=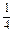
 ,
, =
=
 ,AD与BC相交于点M,设
,AD与BC相交于点M,设 =a,
=a, =b.试用a和b表示向量
=b.试用a和b表示向量 .
.
设两个非零向量a与b不共线,
(1)若 =a+b,
=a+b,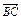 =2a+8b,
=2a+8b,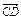 =3(a-b),求证:A、B、D三点共线;
=3(a-b),求证:A、B、D三点共线;
(2)试确定实数k,使ka+b和a+kb共线.
如图所示,若四边形ABCD是一个等腰梯形,AB∥DC,M、N分别是DC、AB的中点,已知 =a,
=a, =b,
=b, =c,试用a、b、c表示
=c,试用a、b、c表示 ,
, ,
, +
+ .
.
定理:若函数 在闭区间[m,n]上是连续的单调函数,且
在闭区间[m,n]上是连续的单调函数,且 ,则存在唯一一个
,则存在唯一一个 。已知
。已知
(1)若 是减函数,求a的取值范围。
是减函数,求a的取值范围。
(2)是否存在 同时成立,若存在,指出c、d之间的等式关系,若不存在,请说明理由。
同时成立,若存在,指出c、d之间的等式关系,若不存在,请说明理由。
已知函数 时取最大值2。
时取最大值2。 是集合
是集合 中的任意两个元素,
中的任意两个元素, 的最小值为
的最小值为 。
。
(1)求a、b的值;
(2)若 的值。
的值。