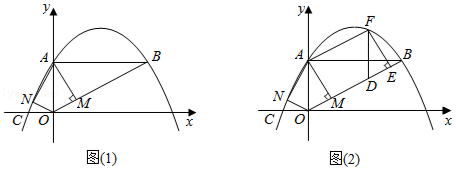解方程: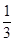 (4-y)=
(4-y)=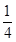 (y+3)
(y+3)
探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有的学习经验,请画出函数 的图象并探究该函数的性质.
|
x |
… |
﹣4 |
﹣3 |
﹣2 |
﹣1 |
0 |
1 |
2 |
3 |
4 |
… |
|
y |
… |
|
a |
﹣2 |
﹣4 |
b |
﹣4 |
﹣2 |
|
|
… |
(1)列表,写出表中 , 的值: , ;
描点、连线,在所给的平面直角坐标系中画出该函数的图象.
(2)观察函数图象,判断下列关于函数性质的结论是否正确(在答题卡相应位置正确的用“√”作答,错误的用“×”作答):
①函数 的图象关于y轴对称;
②当 时,函数 有最小值,最小值为 ;
③在自变量的取值范围内函数y的值随自变量x的增大而减小.
(3)已知函数 的图象如图所示,结合你所画的函数图象,直接写出不等式 的解集.

在数的学习过程中,我们总会对其中一些具有某种特性的数充满好奇,如学习自然数时,我们发现一种特殊的自然数﹣﹣“好数”.
定义:对于三位自然数n,各位数字都不为0,且百位数字与十位数字之和恰好能被个位数字整除,则称这个自然数n为“好数”.
例如: 是“好数”,因为4,2,6都不为0,且 ,6能被6整除;
643不是“好数”,因为 ,10不能被3整除.
(1)判断 , 是否是“好数”?并说明理由;
(2)求出百位数字比十位数字大5的所有“好数”的个数,并说明理由.
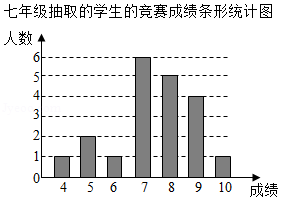
每年的4月15日是我国全民国家安全教育日.某中学在全校七、八年级共800名学生中开展“国家安全法”知识竞赛,并从七、八年级学生中各抽取20名学生,统计这部分学生的竞赛成绩(竞赛成绩均为整数,满分10分,6分及以上为合格).相关数据统计、整理如下:
八年级抽取的学生的竞赛成绩:
4,4,6,6,6,6,7,7,7,8,8,8,8,8,8,9,9,9,10,10.
七、八年级抽取的学生的竞赛成绩统计表
|
年级 |
七年级 |
八年级 |
|
平均数 |
7.4 |
7.4 |
|
中位数 |
a |
b |
|
众数 |
7 |
c |
|
合格率 |
85% |
90% |
根据以上信息,解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)估计该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数;
(3)根据以上数据分析,从一个方面评价两个年级“国家安全法”知识竞赛的学生成绩谁更优异.
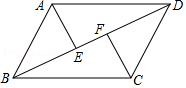
如图,在平行四边形 中, , 分别平分 和 ,交对角线 于点E,F.
(1)若 ,求 的度数;
(2)求证: .
如图(1),在平面直角坐标系中,抛物线 与y轴交于点A,与x轴交于点 ,且经过点B(8,4),连接AB,BO,作 于点M,将 沿y轴翻折,点M的对应点为点N.解答下列问题:
(1)抛物线的解析式为 ,顶点坐标为 ;
(2)判断点N是否在直线AC上,并说明理由;
(3)如图(2),将图(1)中 沿着OB平移后,得到 .若DE边在线段OB上,点F在抛物线上,连接AF,求四边形 的面积.